From Air Canada’s inflight magazine:
And since I’m sure someone will ask, here is, apparently, the only solution they could think of:
Continue reading ‘Worst Puzzle Ever’
Archive for the 'Puzzles' Category
I didn’t think anyone would get it. I was completely stumped myself until I got help from my friends. But Neil got it.
In his words, “We have onomatopoeaic words for the sounds made by all of the animals on the right.”
Or, as I prefer to think of it, the animals on the right all have vocabularies (consisting, in most cases, of a single word) while those on the left do not.
A donkey brays, and when it brays it says hee-haw. The donkey makes it to the right of the line not by virtue of braying, but by saying hee-haw. Thus the elephant, which trumpets, but thereby merely makes a noise (as opposed to saying a word) is consigned to the left.
Lions, tigers, and jaguars all roar, but to the best of my recollection from extensive reading (mostly at about age 5), lions and tigers, when roaring, actually say the word “roar”, while a jaguar merely roars incoherently. Chickens say “cheep”. Hens say “buck-buck-buck” (the act of saying this is called “clucking”). Roosters can crow in either of two dialects: Some say “rrr-rr-rrr-rr-rrrrr” while others (who my five-year-old self considered unbecomingly pretentious) say “cock-a-doodle-doo”. Pretentious they may be, but as a scientist, I am here to record the facts, not to judge them.
Continue reading ‘Yesterday’s Puzzle’
It was said of me in graduate school that “He’s never happy unless he’s making a list”.
My compulsion to make lists has abated over the years, but it lasted long enough that I still find occasional relics lying around.
Recently I ran across the list reproduced below, dating, apparently from my zoology phase, when I was making lists that classified animals according to various criteria. But I was completely unable to recall what criterion had governed this particular list. What rule places the giraffe on the left and the dog on the right?
Continue reading ‘What Was I Thinking?’
Several commenters (n+1, n+2, Trevor, math_geek, EconomistsDoItWithModels, Neil, Mark R., possibly others I’ve overlooked) solved yesterday’s probability puzzle correctly, and you can learn a lot by reading their answers. Here’s my version of their argument:
Among those who are prescribed the medicine, there are five kinds of people, represented by the five non-blacked-out squares in the following chart. A, B, C, D and E are the fractions of the population of each type.
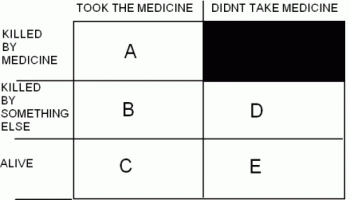
First, we are given that 60% take the medicine, which means 40% don’t take it. That is, A+B+C = 3/5 and D+E = 2/5 . That’s two equations.
Continue reading ‘A Big Answer’
A man goes to the doctor, gets a prescription for a headache medicine, and dies the next day. It’s known that 60% of those who receive these prescriptions actually fill them and take the medicine. It’s also been established by investigators that if the man took the medicine, then there’s a 90% chance it killed him. What’s the probability that he took the medicine and it killed him?
The answer might depend on your auxiliary assumptions, but there is a particularly simple and natural set of auxiliary assumptions that leads to a nice clean answer. And no, that answer is not 54%. (Nor would 54% be an easy answer to defend under any reasonable assumptions I can think of.)
EDIT: I had written here For extra clarity, the phrase “the medicine killed him” should be interpreted to mean that if he hadn’t taken the medicine, he wouldn’t have died. . This seems to be confusing some readers, and I briefly posted an edit here saying to ignore it — but it actually is what I meant to say all along.
Continue reading ‘Another Probability Puzzle’
Today I have a new brain teaser for you. It’s similar in flavor to last week’s brain teaser, but it’s genuinely different, and it’s different in an instructive way. And it stands on its own; you don’t need to have followed last week’s discussion to tackle this.
Here goes: There’s a certain country where everybody wants to have a son. Therefore each couple keeps having children until they have a boy; then they stop. In expectation, what is the ratio of boys to girls?
For those who were here last week, notice that this problem is genuinely different. Last week I asked about the fraction of the population that is female. If we exclude the parents, that’s the ratio G/G+B. Today’s problem asks about the ratio B/G.
Stop here if you don’t want spoilers.
Continue reading ‘A Whole New Brain Teaser’
Last week’s series of posts on boys, girls and population ratios drew an astonishing 850 or more comments, and they’re still coming in. There’s a lot of stuff worth reading in those comments, but the conversation — which is spread out over four threads and often involves several overlapping subconversations — has become difficult to follow. Fortunately, one of our more insightful commenters has volunteered to write a guest post summarizing what he sees as some of the most important discoveries to come out of those discussions. He has signed his guest post “Tom M”, but in the comments, he is simply “Tom”.
Without further ado:
1. Introduction
Steve Landsburg posed a problem in this post at his blog entitled Are You Smarter than Google?. Here was the problem statement:
There’s a certain country where everybody wants to have a son. Therefore each couple keeps having children until they have a boy; then they stop. What fraction of the population is female?
Well, of course, you can’t know for sure, because, by some extraordinary coincidence, the last 100,000 families in a row might have gotten boys on the first try. But in expectation, what fraction of the population is female? In other words, if there were many such countries, what fraction would you expect to observe on average?
As we’ve worked on that problem, one of the points that came up was something called the “extra half boy.”
In this post I’m going to try to summarize what we’ve said about that critter and some related issues.
A key reference, that everybody should read, is What is the expected proportion of girls?, by ‘Thomas Bayes’.
Continue reading ‘The Extra Half Boy’
How rational are you? I once posted a test, based on ideas of the economist Maurice Allais, that most people seem to fail. Today’s test, based on ideas of the economist Dick Zeckhauser and the philosopher Richard Jeffrey, is one that almost everyone fails.
Suppose you’ve somehow found yourself in a game of Russian Roulette. Russian roulette is not, perhaps, the most rational of games to be playing in the first place, so let’s suppose you’ve been forced to play.
Question 1: At the moment, there are two bullets in the six-shooter pointed at your head. How much would you pay to remove both bullets and play with an empty chamber?
Question 2: At the moment, there are four bullets in the six-shooter. How much would you pay to remove one of them and play with a half-full chamber?
In case it’s hard for you to come up with specific numbers, let’s ask a simpler question:
The Big Question: Which would you pay more for — the right to remove two bullets out of two, or the right to remove one bullet out of four?
The question is to be answered on the assumption that you have no heirs you care about, so money has no value to you after you’re dead.
Almost everybody says they’d pay more in the first case than the second. Arguably, that means that in this scenario almost nobody is rational — because a rational person would give the same answer to both questions.
The reason for that is not immediately obvious. To understand it, you’ve got to think about four questions:
Continue reading ‘Another Rationality Test’
As promised, I am providing an update on the status of the various bets that got placed here last week.
The problem is this: In a certain country, each family continues having children until it has a boy, then stops. In expectation, what fraction of the population is female?
The answer is: not 1/2. A more precise answer depends on your additional assumptions — the number of families, the mortality rate, whether the parents count, whether there are grandchildren, etc. It might be possible to engineer those additional assumptions in some way that makes the answer come out to 1/2, but it would surely be impossible to argue that those ad hoc assumptions, whatever they are, are implicit in the statement of the problem.
Pretty much everyone seems to understand this now. (Here‘s one more learning aid, if you’re still struggling.) What, then, are we betting about? Here is a list of all the open and closed bets:
Continue reading ‘Status of the Bets’
It has been said of Lubos Motl that he’s hard to ignore, but it’s always worth the effort. I will, soon enough, take this advice to heart. But not quite yet. Lubos’s penchant for twisting other people’s words, just so he can have something to argue about, is well known and widely remarked. As his most recent victim (though “victim” is of course too strong a word, no actual harm having been done), I thought it would be both fun and instructive to challenge him to a bet. True to form, he continued to bluster but of course refused to back up his misrepresentations with actual cash.
Now of course Lubos will say that it is I who am twisting words, and in particular that I either “changed the question” or “changed the answer” (or both) between the original post and the offer to bet. That, however, won’t wash, since I’ve agreed, as part of the terms of the bet, to let an impartial panel of statistics professors determine the answer to the question as it was originally posed. So even if I had changed the question (which I haven’t), this would prevent me from getting away with it. (And no, I haven’t changed the answer either. If Lubos claims I have, we can put that to the stats profs also.)
I’m feeling annoyed enough to say a little more along these lines, but first I’d like to make it crystal clear that my annoyance does not extend to readers who are still puzzling this out. The problem with Lubos isn’t that he’s got it wrong; it’s that he’s not the least bit interested in getting it right. A few particulars:
Continue reading ‘Slippery Lube’
Last week I posted a little brain teaser that shows up frequently in recreational puzzle books — and reportedly in Google job interviews. The interesting thing about that puzzle is that the “official” answer is wrong. Not only that, but it’s wrong for an interesting reason.
I explained the official answer, I explained exactly where it goes wrong, and I explained how to get the right answer, citing Douglas Zare’s post here as inspiration.
The physicist Lubos Motl, however, still defends the official “50%” answer on his own blog. I am therefore offering to bet him $15,000 that I’m right (with detailed terms described below). If you agree with Lubos, this is your chance to get in on the action. I will take additional bets up to $5000 per person from all comers until such time as I decide to cut this off. You can place your bet by commenting on this post with the amount you’d care to stake. Be sure to include your email address (which does not show up in the post) so I can email you and verify that you’re for real.
Continue reading ‘Win Landsburg’s Money!!!’
I was going to wait a few days before posting the answer to yesterday’s puzzler, but we’re up well over 100 comments already, the holidays are almost upon us, and I think it’s time to settle this so you can all give your full attention to whatever festivities you’ve got coming up.
Here’s the puzzle again:
More precisely: What fraction of the population should we expect to be female? That is, in a large number of similar countries, what would be the average proportion of females?
Stop reading here if you don’t want spoilers:
Continue reading ‘A Big Answer’
There’s a certain country where everybody wants to have a son. Therefore each couple keeps having children until they have a boy; then they stop. What fraction of the population is female?
Well, of course, you can’t know for sure, because, by some extraordinary coincidence, the last 100,000 families in a row might have gotten boys on the first try. But in expectation, what fraction of the population is female? In other words, if there were many such countries, what fraction would you expect to observe on average?
I first heard this problem decades ago, and so, perhaps, did you. It comes up in job interviews at places like Google. The answer they expect is simple, definitive and wrong.
Continue reading ‘Are You Smarter Than Google?’
Last week I posed a (perhaps imperfectly remembered) problem from Nick Kiefer’s course on Decision Theory. I’m very sorry that I haven’t found time to work out a complete solution (or even to read carefully through all the comments). Today I’ll post some hints from my notes toward a solution. Warning One: Only the math nerds will care about this post. Warning Two: This has all been double checked, but none of it’s been triple checked. It could be wrong.
The goal is to guess Nick’s secret number, which is drawn randomly from a uniform distribution on the numbers from 0 to 100. Each day, he draws a new “Number of the Day” and tells you whether it’s larger or smaller than the secret number.
Continue reading ‘That Decision Theory Problem’
Many years ago, when I was teaching at Cornell, my then-colleague Nick Kiefer kept me endlessly amused with the creative assignments he dreamed up for the students in his Decision Theory class. I’m reporting this from memory, so I don’t guarantee that I have it exactly right, but I think this was one of those problems:
- On Day Zero (before classes start), Nick uses his pocket calculator to generate, at random, a secret number between 0 and 100. This number is drawn from a uniform distribution, which means (roughly) that the drawing is unbiased, so any number is as likely to come up as any other. The students’ job is to guess this number.
- On Day One — the first day of class — Nick uses his pocket calculator to generate a Number of the Day. He doesn’t tell the students what the Number of the Day is, but he does tell them whether it’s larger or smaller than the secret number.
- On Days Two, Three, and so forth, he does the same thing. He generates a Number of the Day and announces whether it’s bigger or smaller than the secret number.
- You, the student, can submit your guess on the day of your choice.
- You are then assessed two penalties. The first penalty is equal to the square of the error in your guess. So if the correct number is 3 and your guess is 5, your penalty is 22, or 4. The second penalty is equal to the natural logarithm of the day when you submit your guess. So if you submit your guess on Day 7, your penalty is the log of 7, which is 1.94591.
- These penalties are subtracted from some some fixed number of points that you’re given to start out with (say 1000). The result, after the subtraction, is your score for the assignment. This score counts for a significant fraction of your course grade.
Continue reading ‘How to Decide’
It’s been “reasonable doubt” week here at The Big Questions. We’ve talked about recognizing reasonable doubt when you see it, about what the standard should be, and about what the standard for determining the standard should be.
This raises the question: What is the standard? Here’s the weird part: Nobody knows. The judges won’t tell you and neither will the legislators. If you’re on a jury, you’re on your own.
Now you might say that that’s a fine thing. We want to leave it to jurors to set this standard. Under that theory, a juror has two separate questions to answer. One is “How doubtful am I?” and the other is “How much doubt counts as reasonable?”. But I don’t believe anyone actually subscribes to that theory.
Here’s why I say that: Suppose that in a murder trial, the foreman of the jury reports back to the judge that the jurors have agreed that there’s a 15% chance the defendant is guilty, and that they consider 15% to be beyond a reasonable doubt. Therefore they have unanimously voted to convict. I am not a lawyer, but I will cheerfully bet you that in any such case, the judge would throw the conviction out in a hurry, on the grounds that 15% is not at all beyond reasonable.
In other words, the judge does not subscribe to the theory that it’s entirely up to the jurors to set the reasonable doubt standard. Moreover, the judge would throw out the verdict at 16% or 17% or 18% and so on up to …. what? Well, up to some number. That number is a standard that the judge is prepared to enforce. What is that number? I bet the judge won’t tell you. The question is: Why not? Why doesn’t the judge say something like “You should convict if you are at least 90% certain the defendant is guilty”?
Continue reading ‘Blinded Justice’
Two days ago, we asked whether lawyers (or anyone else) can recognize reasonable doubt (or its absence) when they see it. Yesterday we stepped back to ask the question: What is the right standard for “reasonable doubt”? Should you convict when the probability of guilt is 70%? 80%? 90%? Of course the answer might vary with the crime and the prospective punishment. To keep this discussion concrete, I’ll focus on capital punishment for murder, and to keep it simple, I’ll pretend that no other punishment is available (so that the only choices are “acquit” and “execute”).
Today I want to take yet another step back and ask: What is the right standard for deciding the right standard? Here are two possible meta-standards:
1. Minimize the suffering of innocents.
2. Minimize suffering.
The difference is in whether we choose to care about the suffering of murderers.
Continue reading ‘Reasoning About Reasonableness’
Yesterday, I posed these questions:
Here I have a couple of urns. The one on the left contains 70 red balls and 30 black. The one on the right contains 30 red and 70 black.
While you weren’t looking, I reached into one of these urns and randomly drew out a dozen balls…4 of them were red and 8 were black.1. If you had to guess, which urn would you guess I drew from?
2. What’s your estimate of the odds that you’re right?
3. Do you think you’re right beyond a reasonable doubt?
I stole this problem from the decision theorist Howard Raiffa, with some minor changes (he used bags instead of urns, and green and white balls instead of red and black — and he drew his twelve balls with replacement, rather than all at once, which has only a tiny effect on the probability). Here, with appropriate minor wording changes, is what Raiffa had to say:
Continue reading ‘Reasonable Doubts’
Here I have a couple of urns. The one on the left contains 70 red balls and 30 black. The one on the right contains 30 red and 70 black.
While you weren’t looking, I reached into one of these urns and randomly drew out a dozen balls. As you can see, 4 of them were red and 8 were black.
Here are three questions that I think you ought to be able to answer if you want to be in the business of assessing evidence:
- If you had to guess, which urn would you guess I drew from?
- What’s your estimate of the odds that you’re right?
- Do you think you’re right beyond a reasonable doubt?
Further discussion to follow later in the week. (Hat tip to Howard Raiffa, who will also figure in the upcoming discussion.)
1) I just had an extremely pleasant walk around the Beale Street area in Memphis, which strikes me, roughly, as Bourbon Street without the urine. (Also without the trash and the high general level of obnoxiousness — though also of course without the magnificent architecture, etc.) Yes, I realize it’s also a different musical genre (though in both cases it’s a sub-genre of “too loud”). But it’s astonishing to me how clean the streets are here, and how well-behaved the crowds, compared to what I’ve seen in Louisiana. If they can do that here, why can’t they do it there?
2) This weekend marks the anniversary of a world-changing event — an event that might be of particular interest to readers of The Big Questions, both the book and the blog. Who can tell me what event I have in mind? (Hint: It’s an anniversary ending in zero.) I’ll blog the answer on Monday.
3) The discussion of the Allais paradox rages on in comments on multiple posts. For the few of you who have not yet tuned this out, my latest comment is an attempt to cut through the fog and identify the locus of some commenters’ confusion, or disagreement, or both. I think it will very much help focus the discussion if the dissenters could tell us where they stand on these questions. (My answers are all “yes”.)
Leonard Jimmie Savage was a pioneer in modern decision theory and a disciple of Frank Plumpton Ramsey, whose story occupies the final chapter of The Big Questions.
In 1954, Savage wrote a lovely and highly influential little book called The Foundations of Statistics, which starts with six simple axioms about human preferences — one of which says that if you prefer a dog to a cat, then you’ll prefer an 11% chance of a dog to an 11% chance of a cat (and likewise for any other percentage). From these axioms, he drew deep and surprising conclusions about human behavior. This work underlies much of modern game theory, decision theory and economics in general.
According to legend (and I have reason to suspect this legend is actually true), Professor Savage was giving a talk one day when he was interrupted by the French econometrician (and then-future Nobel Prize winner) Maurice Allais, who asked Savage if he’d be willing to answer two questions about his own preferences. Savage said sure. These were the questions:
Continue reading ‘The Noble Savage’
Can ignorance be bliss?
There is allegedly a tradition of issuing a blank cartridge to one (randomly chosen) member of each firing squad, so that no shooter knows for certain that he contributed to a death. Let’s assume that tradition really exists and let’s assume that it exists because the shooters want it. Does that prove that shooters (at least in some instances) value ignorance?
Not necessarily. It might just mean that each shooter prefers a 5/6 chance of firing a real bullet over a 100% chance of firing a real bullet. That’s not the same thing as preferring to be ignorant.
So here’s the key experiment. Offer the shooters a choice:
Continue reading ‘Ignorance, Bliss, and Rationality Re-Redux’
The rationality quiz that I posted on Tuesday has drawn a lot of comments from folks who think they can reconcile inconsistent answers by appealing to risk aversion. That’s surely incorrect. To see why, let’s start with another quiz.
Question 0: Which do you like better, dogs or cats?
Economists would not presume to declare either choice an irrational one. There’s no accounting for tastes.
Now I have two more questions for you:
Continue reading ‘Rationality Redux’
The death this week of Nobel laureate (and relativity denier!) Maurice Allais reminds me that I’ve been meaning to blog about Allais’s famous challenge to the way economists think about rational decision making.
I’m going to ask you two questions about your preferences. In neither case is there a right or a wrong answer. A perfectly rational person could answer either question either way. But I do want you to think about your answers, and to write them down before you read any further.
Question 1: Which would you rather have:
- A million dollars for certain
- A lottery ticket that gives you an 89% chance to win a million dollars, a 10% chance to win five million dollars, and a 1% chance to win nothing.
Try taking this seriously. What would you actually do if you faced this choice? Don’t bother trying to figure out the “right” answer, because there is no right answer. Some perfectly rational people choose A, and other perfectly rational people choose B.
Okay, ready for the next question?
Question 2: Which would you rather have:
- A lottery ticket that gives you an 11% chance at a million dollars (and an 89% chance of nothing)
- A lottery ticket that gives you a 10% chance at five million dollars (and a 90% chance of nothing)
Once again, this is a matter of preference. There is no right or wrong answer. But decide what your answer is and write it down before you continue.
Continue reading ‘How Rational Are You?’
If you like this blog, then you either are or should be a fan of the late Martin Gardner, the long-time “Mathematical Games” columnist for Scientific American. On the 21st of October (what would have been Gardner’s 96th birthday), “Gatherings for Gardner” will take place around the world, where fans can share their favorite puzzles, ideas, magic tricks and reminiscences in what’s being billed as a global “celebration of mind”. You’re welcome to attend one of these events — or to host one.
(Potential attendees would surely benefit from a list of locations in lieu of having to navigate that idiotic map, but that’s what’s there.)
It was at a previous Gathering for Gardner that puzzle designer Gary Foshee posed his notoriously tricky probability puzzle about the mom with a son born on a Tuesday. (Spoilers here.) If you host or attend a gathering, do come back here and share your favorite finds.
You’re lost in a forest. What’s the best way to get out?
The great macroeconomist Bob Lucas once asked me this question, and I had no answer for him. I still don’t.
The assumption is that you know the size and shape of the forest, but you don’t know where you are or which way you’re facing. And the forest is so dense that you can never see any significant distance in front of you. What path should you follow?
Continue reading ‘Escaping the Forest’
Last week I posed this problem:
Several commenters did a wonderful job of explaining the answer. Let me just add a few words on the issue of “How can Tuesday be relevant?”
If the Tuesday part weren’t there, the problem would be easy. With two children, there are three equally likely ways to have (at least) one boy: The children in birth order might be Boy/Boy, Boy/Girl, or Girl/Boy. That gives a 1/3 chance of Boy/Boy.
So what does “Tuesday” have to do with it? Answer: Having (at least) one Tuesday boy is a lot more likely when you’ve got two boys than when you’ve got only one. So among those moms with a Tuesday boy, the Boy/Boy moms outnumber either of the other types. The three possibilities aren’t equally likely anymore.
Continue reading ‘A Big Answer’
With a hat tip to the mathematician John Baez, who in turn tips his hat to the science fiction author Greg Egan, who in turn credits the journalist Alex Bellos, who got this from the puzzle designer/collector Gary Foshee (who seems to have no website):
(For those who want more precision: We gather all those women in the world who have exactly two children, tell each of them to “go home unless you have a boy born on a Tuesday”, and select a woman randomly from those who remain. Assume that births are equally likely to occur on any day of the week, and that on any given day, boys and girls are equally likely.)
Yesterday’s pop quiz posed this question:
Suppose that an acre of land in Iowa can yield either 50 bushels of wheat or 100 bushels of corn, while an acre of land in Oklahoma can yield either 20 bushels of wheat or 30 bushels of corn.
Which state has the comparative advantage in growing wheat? Which state has the comparative advantage in growing corn?
Suppose the residents of each state consume 200 bushels of wheat and 360 bushels of corn. If, instead of pursuing policies of self-sufficiency, each state specializes in its area of comparative advantage, how many acres of Iowa and Oklahoma farmland are freed up for other uses?
Quite a few people got this right in comments. In Iowa, the opportunity cost of a bushel of wheat is 2 bushels of corn. In Oklahoma, the opportunity cost of a bushel of wheat is 3/2 bushels of corn. Becauses 3/2 is less than 2, Oklahoma is the low-cost wheat producer, which is the same thing as saying that Oklahoma has the comparative advantage in wheat.
Continue reading ‘Pop Answers’
Commenting on this essay by former Intel chief Andy Grove, Tyler Cowen writes that “Only he who first shows he understands comparative advantage has license to partially reject it.”
Hear hear. When someone says “I understand comparative advantage, but in this case it doesn’t apply”, or “I understand comparative advantage but in this case it is overridden by other considerations”, my experience tells me that you can be nearly sure you’re talking to someone who does not in fact understand comparative advantage.
