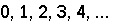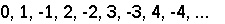You’re lost in a forest. What’s the best way to get out?
The great macroeconomist Bob Lucas once asked me this question, and I had no answer for him. I still don’t.
The assumption is that you know the size and shape of the forest, but you don’t know where you are or which way you’re facing. And the forest is so dense that you can never see any significant distance in front of you. What path should you follow?
Continue reading ‘Escaping the Forest’
Over the course of my childhood, I remember asking exactly one intelligent question. Unfortunately, I couldn’t make my parents understand what I was asking. Perhaps it was that frustration that deterred me from ever formulating an intelligent question again.
I was, I think, six years old at the time, and my question was this: If you’re traveling at 50 miles an hour at 1:00, and you’re traveling at 70 miles an hour at 2:00, must there be a time in between when you’re traveling exactly 60 miles an hour?
What made this question intelligent—and probably what made it incomprehensible to my parents—was that I was very keen to distinguish it from the question of whether your speedometer would have to pass through the 60-mile-an-hour mark. It seemed clear to me that the answer to that one was yes—that even if your true velocity could somehow skip directly from 50 to 70, the speedometer needle, in the course of whipping around from one reading to the other, would have to pass through the midpoint.
I quite vividly remember worrying that my question about your speed would be misinterpreted as a question about your speedometer, a question to which I thought the answer was obvious and therefore could only be asked by a very stupid person—a very stupid person for whom I did not wish to be mistaken. Therefore I prefaced the question with a long discourse on how it was thoroughly obvious to me that if your speedometer reads 50 miles an hour at one time and 70 miles an hour at another, then surely it must pass through 60 on the way, but that this was not not not not not the question I was about to ask, which concerned your actual speed and not the measurement thereof. By the time I got around to formulating the question itself, my parents (or at least my father; I don’t remember whether my mother was present) had quite understandably given up on figuring out what I was trying to get at.
This is an extremely elementary post about numbers. (“Numbers” means the natural numbers 0,1,2 and so forth.) It is a sort of sequel to my three recent posts on basic arithmetic, which are here, here and here. But it can be read separately from those posts.
Today’s question is: Do numbers exist? The answer is: Of course, and I don’t believe there’s much in the way of serious doubt about this. You were familiar with numbers when you were five years old, and you’ve been discovering their properties ever since. Extreme skepticism on this point is almost unheard of among mathematicians or philosophers, though it seems to be fairly common among denizens of the Internet who have gotten it into their head that extreme skepticism makes them look sophisticated.
Let me be clear that I am not (yet) asking in what sense the natural numbers exist — whether they have existed since the beginning of time, or whether they exist outside of time, or whether they exist only in our minds. Those are questions that reasonable people disagree about (and that other reasonable people find more or less meaningless.) We can — and will — come back to those questions in future posts. For now, the only question: Do the natural numbers exist? And the answer is yes. Or better yet — if you believe the answer is no, then there’s obviously no point in thinking about them, so why are you reading this post?
Continue reading ‘Basic Arithmetic: On What There Is’
 |
 |
 |
 |
Congratulations to the 2010 Fields Medalists, announced yesterday in Hyderabad. Elon Lindenstrauss, Ngo Bau Chau, Stanislav Smirnov, and Cedric Villani have been awarded math’s highest honor. (Up to four medalists are chosen every four years.)
My sense going in was that Ngo was widely considered a shoo-in, for his proof of the Fundamental Lemma of Langlands Theory. Do you want to know what the Fundamental Lemma says? Here is an 18-page statement (not proof!) of the lemma. The others were all strong favorites. Nevertheless:
Continue reading ‘Wikipedia Fail’
Today let’s talk about consistency.
Suppose I show you a map of Nebraska, with as-the-crow-flies distances marked between the major cities. Omaha to Lincoln, 100 miles. Lincoln to Grand Island, 100 miles. Omaha to Grand Island, 400 miles.
You are entitled to say “Hey, wait a minute! This map is inconsistent. The numbers don’t add up. If it’s 400 miles straight from Omaha to Grand Island, then there can’t be a 200 mile route that goes through Lincoln!”
So a map can be inconsistent. (It can also be consistent but wrong.) Nebraska itself, however, can no more be inconsistent than the color red can be made of terrycloth. (Red things can be made of terrycloth, but the color red certainly can’t.)
With that in mind, suppose I give you a theory of the natural numbers — that is, a list of axioms about them. You might examine my axioms and say “Hey! These axioms are inconsistent. I can use them to prove that 0 equals 1 and I can also use them to prove that 0 does not equal 1!” And, depending on the theory I gave you, you might be right. So a theory can be inconsistent. But the intended model of that theory — the natural numbers themselves — can no more be inconsistent than Nebraska can. Inconsistency in this context applies to theories, like the Peano axioms for arithmetic, not to structures, like the natural numbers themselves.
Continue reading ‘Basic Arithmetic, Part III: The Map is Not the Territory’
Today’s mini-lesson in the foundations of mathematics is about the key distinction between theories and models.
The first thing to keep in mind is that mathematics is not economics, and therefore the vocabulary is not the same. In economics, a “model” is some sort of an approximation to reality. In mathematics, the word model refers to the reality itself, whereas a theory is a sort of approximation to that reality.
A theory is a list of axioms. (I am slightly oversimplifying, but not in any way that will be important here.) Let’s take an example. I have a theory with two axioms. The first axiom is “Socrates is a man” and the second is “All men are mortal”. From these axioms I can deduce some theorems, like “Socrates is mortal”.
That’s the theory. My intended model for this theory is the real world, where “man” means man, “Socrates” means that ancient Greek guy named Socrates, and “mortal” means “bound to die”.
But this theory also has models I never intended. Another model is the universe of Disney cartoons, where we interpret “man” to mean “mouse”, we interpret “Socrates” to mean “Mickey” and we interpret “mortal” to mean “large-eared”. Under that interpretation, my axioms are still true — all mice are large-eared, and Mickey is a mouse — so my theorem “Socrates is mortal” (which now means “Mickey is large-eared”) is also true.
Continue reading ‘Basic Arithmetic, Part II’
With the P=NP problem in the news, this seems like a good time to revisit the distinction between truth and provability.
Start with this P=NP-inspired question:
I don’t need you to answer that question. I just want you to answer an easier question:
If you said yes (as would be the case, for example, if you happen to be sane), then you have recognized that statements about arithmetic can be either true or false independent of our ability to prove them from some set of standard axioms. After all, nobody knows whether the standard axioms of arithmetic (or even the standard axioms for set theory, which are much stronger) suffice to settle Question 1. Nevertheless, pretty much everyone recognizes that Question 1 must have an answer.
Let’s be clear that this is indeed a question about arithmetic, not about (say) electrical engineering. A computer program is a finite string of symbols, so it can easily be encoded as a string of numbers. The power to factor quickly is a property of that string, and that property can be expressed in the language of arithemetic. So Question 1 is an arithmetic question in disguise. (You might worry that phrases like “quickly” or “substantially faster” are suspiciously vague, but don’t worry about that — these terms have standard and perfectly precise definitions.)
Continue reading ‘Basic Arithmetic’
Something momentous happened this week. Of this I feel certain.
A little over a week ago, HP Research Scientist Vinay Delalikar claimed he could settle the central problem of theoretical computer science. That’s not the momentous part. The momentous part is what happened next.
Deolalikar claimed to prove that P does not equal NP. This means, very roughly, that in mathematics, easy solutions can be difficult to find. “Difficult to find” means, roughly, that there’s no method substantially faster than brute force trial-and-error.
Plenty of problems — like “What are the factors of 17158904089?” — have easy solutions that seem difficult to find, but maybe that’s an illusion. Maybe there’s are easy solution methods we just haven’t thought of yet. If Deolalikar is right and P does not equal NP, then the illusion is reality: Some of those problems really are difficult. Math is hard, Barbie.
So. Deolalikar presented (where “presented” means “posted on the web and pointed several experts to it via email”) a 102 page paper that purports to solve the central problem of theoretical computer science. Then came the firestorm. It all played out on the blogs.
Dozens of experts leapt into action, checking details, filling in logical gaps, teasing out the deep structure of the argument, devising examples to illuminate the ideas, and identifying fundamental obstructions to the proof strategy. New insights and arguments were absorbed, picked apart, reconstructed and re-absorbed, often within minutes after they first appeared. The great minds at work included some of the giants of complexity theory, but also some semi-outsiders like Terence Tao and Tim Gowers, who are not complexity theorists but who are both wicked smart (with Fields Medals to prove it).
The epicenter of activity was Dick Lipton’s blog where, at last count, there had been been 6 posts with a total of roughly 1000 commments. How to keep track of all the interlocking comment threads? Check the continuously updated wiki, which summarizes all the main ideas and provides dozens of relevant links!
I am not remotely an expert in complexity theory, but for the past week I have been largely glued to my screen reading these comments, understanding some of them, and learning a lot of mathematics as I struggle to understand the others. It’s been exhilarating.
Continue reading ‘O Brave New World!’
The really big news from Hewlett Packard this week was not the dismissal of CEO James Hurd but the announcement by HP Labs researcher Vinay Deolalikar that he has settled the central question in theoretical computer science.
That central question is called the “P versus NP” problem, and for those who already know what that means, his claim (of course) is that P does not equal NP. For those who don’t already know what that means, “P versus NP” is a problem about the difficulty of solving problems. Here‘s a very rough and imprecise summary of the problem, glossing over every technicality.
Deolalikar’s paper is 102 pages long and less than about 48 hours old, so nobody has yet read it carefully. (This is a preliminary draft and Deolalikar promises a more polished version soon.) The consensus among the experts who have at least skimmed the paper seems to be that it is a) not crazy (which already puts it in the top 1% of papers that have addressed this question), b) teeming with creative ideas that are likely to have broad applications, and c) quite likely wrong.
As far as I’m aware, people are betting on point c) not because of anything they’ve seen in the paper, but because of the notorious difficulty of the problem.
And when I say betting, I really mean betting. Scott Aaronson, whose judgment on this kind of thing I’d trust as much as anyone’s, has publicly declared his intention to send Deolalikar a check for $200,000 if this paper turns out to be correct. Says Aaronson: “I’m dead serious—and I can afford it about as well as you’d think I can.” His purpose in making this offer?
Continue reading ‘P, NP and All That’
Yesterday I answered one of Coupon Clipper‘s questions about Godel’s Theorem. Today I’ll tackle the other: Does Godel’s Theorem matter on a day-to-day basis to practicing mathematicians?
And the answer is: Of course not. Mathematicians care about what’s true, not about what’s provable from some arbitrary set of axioms. (Of course this is an overgeneralization; some mathematicians have built distinguished careers on worrying about what’s provable from various sets of axioms. But they are a small minority.) Godel’s Theorem says that not all true things are provable. But for the most part, we’re happy just to know they’re true.
The flashiest example I can give you—and one I’ve used on this blog before—is Fermat’s Last Theorem, which says that no equation of the form xn + yn = zn has any solutions, as long as n is at least 3 and x, y and z are non-zero. Proving this was the was most famous unsolved problem in mathematics for 350 years until it was solved (to much public fanfare) by Frey, Serre, Ribet and Wiles in the 1980’s and 1990’s.
We know from that work that Fermat’s Last Theorem is true. However, we still don’t know whether Fermat’s Last Theorem follows from the standard axioms for arithmetic. And—this is the point—very few mathematicians care very much, at least by comparison to how much they care about the theorem itself. (Here is one of my favorite papers on the subject. Tellingly, the author is a philosopher.)
Continue reading ‘Godel, Fermat, Hercules’
The occasional commenter who goes by the name Coupon Clipper has emailed me some interesting questions about Godel’s Theorem. I think I’ll answer them here.
The first question is about first-order versus second-order logic, so let me explain the distinction. When we reason formally about arithmetic, we need to clearly specify the ground rules. This means, among other things, specifying the language and grammar we’re allowed to use. A very simple language might allow us to say things like “2 + 3 = 5” or “8 is an even number”. With a language like that, you could talk about a lot of sixth grade arithmetic, but you wouldn’t be able to say anything very interesting beyond that. To talk about the questions mathematicians care about, you need a language that contains words like “every”, as in Every number can be factored into primes or Every number can be written as a sum of four squares or Every choice of positiive numbers x, y, and z will yield a non-solution to the equation x3+y3=z3 . That language is called first-order logic.
With first order logic we can specify a set of axioms, and then follow a prescribed set of rules to deduce consequences. For example, if you’ve already established that every number is a sum of four squares, then you’re allowed to conclude that 1,245,783 is a sum of four squares. (The general rule is that if you’ve proved that every number has some particular property, then you’re allowed to conclude that any particular number has that property.)
Continue reading ‘First Things and Second Things’
I’ve just finished reading The Girl Who Played with Fire, the second book in the series that begins with The Girl with the Dragon Tattoo. I’m not giving away any significant plot point when I tell you that there’s a character who works on Fermat’s Last Theorem as a hobby, or that the book was clearly written (or perhaps translated) by somebody with no clue how mathematics works or what Fermat’s Last Theorem is about. I particularly liked the reference to Andrew Wiles using the “world’s most complicated computer program” to solve the problem. It’s my understanding that Andrew barely even uses email. And certainly if you understood anything about the nature of the problem and/or the solution, you’d recognize the absurdity of trying to tackle it with a complicated computer program.
Be that as it may, I finished the novel with a few hours left to spare, so of course I was inspired to work on Fermat’s Last Theorem, or at least on the simplest cases. The problem, if you’ll recall, is to show that there are no integer solutions to any of the equations x3+y3=z3 , x4+y4=z4 and so on, except for the so-called trivial solutions in which one or more variables take the value zero.
Continue reading ‘The Girl Who Played With Numbers’
If there is a God, this is the closest you’ll ever come to hearing Him sing. Let me explain.
Continue reading ‘The Music of the Primes’
My colleague Ralph Raimi is witty, acerbic and wise about many things, but particularly about mathematics education. A little time spent browsing around his web page will reap ample rewards in the form of both entertainment and edification. Today I’d like to share a little passage he sent me by email:
I have never tried to count the times I have read a newspaper article explaining that students are bored with math that has no visible practical application, and follows with an example of a teacher, or club, that rectifies the situation in some novel and engaging way.
In the present case a class has built a sculpture that resembles a graph of a modulated wave motion. Of all the practical, real-world
applications of mathematics! It is as practical as a snowman.Why doesn’t anyone ask for real-world applications of table tennis? What a bore any game must be, that has no real-world application! Why do kids stand for it? Ping-pong again? Ugh.
But I can think of something: Let’s all make a model of a ping-pong ball in the school yard, seventy feet high, blocking all the entrances and thus preventing all us students from entering the (ugh) school. Then we can take our fishing poles and torn straw hats out from under our beds and, with the hats on our heads and fishing poles over our shoulders, all traipse together down the dusty road to Norman Rockwell’s house.
Yesterday I told you about one of the deepest problems in arithmetic. Today I’ll explain how you can help solve it.
We’re on the hunt for ABC triples. A brief recap: We start with an equation of the form A+B = C, where A, B and C have no factors in common. We find all the primes that divide A, B or C, multiply them together and call the result D. The goal is to find examples where C is bigger than D.
If I start with 2+243=245, the primes are 2 (which divides 2), 3 (which divides 243), 5 (which divides 245) and 7 (which also divides 245), so D = 2 x 3 x 5 x 7 = 220, and C (that is, 245) is bigger than D. Success! We’ve found an ABC triple.
We want more. A full understanding of ABC triples would allow us to solve some of the hardest open problems in arithmetic. More importantly, the reason we’d be able to solve those problems is that we’d understand arithmetic itself a whole lot better.
The first step is to find a whole lot of examples to help researchers guess at the underlying patterns.
That’s where you come in.
Continue reading ‘ABC at (Your) Home’
Some of the hardest problems in arithmetic are those that relate multiplication to addition. For example: Is every even number the sum of two primes? This is most assuredly a hard problem—mathematicians have been tackling it for centuries and so far nobody’s solved it. And it relates multiplication to addition. As soon as you talk about primes, you’re (implicitly) talking about multiplication, and of course when you talk about sums, you’re talking about addition.
Or: How many ways can you write the number 2 as the difference of two primes? You can write 2 = 5-3, or 2 = 7-5, or 2 = 13-11. That’s three so far. How many more are there? The betting is that the answer is “infinitely many”, but nobody knows for sure. This problem has stumped some of the best and the brightest not just for centuries but for millennia. And again it relates multiplication to addition. (Well, it relates multiplication to subtraction, but of course subtraction is just addition in reverse.)
The ABC problem has only been around for a few decades, but it’s in many ways the most interesting and important of the bunch. Tomorrow I’ll explain how you can help solve this problem. Today I’ll explain what the problem is.
Continue reading ‘The ABC’s of Arithmetic’
During our brief intermission last week, commenters chose to revisit the question of whether arithmetic is invented or discovered—a topic we’d discussed here and here. This reminded me that I’ve been meaning to highlight an elementary error that comes up a lot in this kind of discussion.
It is frequently asserted that the facts of arithmetic are either “tautologous” or “true by definition” or “logical consequences of the axioms”. Those are three different assertions, and all of them are false. (This is not a controversial statement.)
The arguments made to support these assertions are not subtly flawed; they are overtly ludicrous. Almost always, they consist of “proof by example”, as in “1+1=2 is true by definition; therefore all the facts of arithmetic are true by definition”. Of course one expects to stumble across this sort of “reasoning” on the Internet, but it’s always jarring to see it coming from people who profess an interest in mathematical logic. (I will refrain from naming the worst offenders.)
So let’s consider a few facts of arithmetic:
Continue reading ‘Just the Facts’
Blogging, as you might have heard, is changing the face of the media. It may also be changing the face of mathematical research. For the first time ever, a substantial mathematical problem has been solved via an accumulation of blog comments, all building on each other. Could this be the future of mathematical research?
Before I explain the problem, let’s talk a little about tic-tac-toe. As you probably figured out long ago, intelligent players of ordinary tic-tac-toe (on a 3 by 3 board) will invariably battle to a draw. But, as you probably also figured out, not every game ends in a draw, because not every player is intelligent.
On the other hand, if we blacken out the three squares on the main diagonal and don’t allow anyone to play there (so the game ends when the remaining six squares are filled, then every game is sure to end in a draw. There’s simply no way to get three in a row when you’re not allowed to play on the diagonal:
Continue reading ‘Blogging, Tic Tac Toe and the Future of Math’
In high school, we used to play four-dimensional tic-tac-toe. The board looks like this:
Here each four-by-four subsquare is an ordinary tic-tac-toe board (except that it’s four-by-four instead of the traditional three-by-three). You should think of the four subsquares in the first column (or any other column) as stacked above each other in the third dimension. The red x’s form a vertical line in that direction, so if you manage to place four x’s in those positions, you’re a winner.
You should also think of the four subsquares in the first row as stacked above each other in yet another dimension. The red o’s form a diagonal line passing from the bottom left to the top right (using “bottom” and “top” to refer to directions in this fourth dimension). And the black x’s form another kind of diagonal line, passing from one corner to another through all four dimensions. So there are a lot of ways to win this game.
Continue reading ‘Tic Tac Toe in Four Dimensions’
It’s a bit of an odd feeling to be reading a novel and stumble upon yourself as a character. Well, at least a well-disguised version of yourself. The novel is Victor Snaith’s The Yukiad, and the character is a large Scotsman named Pans who tugs at his earrings when he becomes agitated. I am neither Scottish, nor earringed, nor particularly large, but I suspect that Pans, viewed through the haze of poetic license, is I.
When we meet Pans, he is hovering over a glass contraption—a perpetual motion machine, really—consisting of a circular tube containing several colored beads, which travel around the tube, some clockwise, some counterclockwise, all at the same speed, bouncing off each other in perfectly elastic collisions whenever they collide. Pans is currently tugging at his earrings so hard as to cause some concern for the integrity of his earlobes, as he ponders the following question:
But wull tha’ aver gut bark to weer tha’s started, at a’, at a’?
Well, okay, maybe I’m not Pans. Maybe I’m the character Sherloch Humes, a “trim but rather wrinkled gentleman in worsteds”, who calculates for Pans’s benefit that “the configuration of beads is guaranteed to have exactly replicated itself by the year two thousand and nineteen”. I believe that I am the inspiration for one of these characters and that the mathematician Leonid Vaserstein (who is neither Scottish nor wrinkled) is the inspiration for the other, and here is why:
Continue reading ‘The Yukiad, Perpetual Motion and Me’
Wall Street quants are always trying to dream up new financial products that nobody’s figured out how to regulate. Sooner or later, I suppose, one of them will come up with a bank account that pays imaginary interest. You deposit a dollar and a year later you get an interest payment of i. That’s not “i for interest”; it’s the square root of minus one. I have no idea what that means for economics, but thinking about it is a good way to understand Euler‘s (or, the historical record being unclear, perhaps Johann Bernoulli‘s) breathtakingly beautiful formula
| eiπ = -1 |
Continue reading ‘Financial Imagineering’
Professor Joseph Weiler, who is facing criminal charges in France for posting a mildly negative book review on a web site he edits, has asked supporters to search out and email him copies of even more negative reviews (presumably of academic writing), to submit to the court as evidence that this sort of thing happens all the time.
The review I’ll be emailing is a classic of the genre. It was written by Andre Weil, one of the most influential mathematicians of the twentieth century, and possibly the most erudite person who ever lived. Here’s how I described Weil shortly after his death:
Continue reading ‘The Hunting of the Snark’
Today is the 165th birthday of Georg Ferdinand Ludwig Philipp Cantor, the mathematician who indirectly inspired me to major in math. In my first few semesters of college, I was at best an indifferent student, finding little inspiration in the humanities majors I was bouncing around among, playing a prodigious amount of pinball, and attaining (according to rumor) history’s first-ever grade of C in Peter Regenstrief‘s Poltical Science 101. Then one day, my friend Bob Hyman happened to mention that some infinities are larger than others, and set my life on track. This—the vision of Georg Cantor—was something I had to know more about. Before long I was immersed in math.
What does it mean for some infinities to be larger than others? Well, for starters, some infinite sets can be listed, while others are too big to list. The natural numbers, for example, are already packaged as a list:
 |
The integers, by contrast (that is, the natural numbers plus their negatives) aren’t automatically listed because a list, by definition, has a starting point, whereas the integers stretch infinitely far in both directions. But we can fix that by rearranging them:
 |
So the integers can also be listed.
Continue reading ‘Split Infinities’
In 1958, the 30-year-old Alexandre Grothendieck stunned the International Congress of Mathematicians with his audacious proposal to remake the foundations of algebraic geometry, vastly expanding the scope of the field, subsuming all of commutative algebra and algebraic number theory, and paving the way for the solution of the elusive Weil conjectures, then considered decades or centuries out of reach. No mathematical vision had ever been more radical or more ambitious. Someday I will blog about that vision. Today’s post is about genius, eccentricity and intellectual property.
Continue reading ‘Bringing in the Sheaves’
A musician wakes from a terrible nightmare. In his dream he finds himself in a society where music education has been made mandatory…Since musicians are known to set down their ideas in the form of sheet music, these curious black dots and lines must constitute the “language of music”. It is imperative that students become fluent in this language if they are to attain any degree of musical competence; indeed it would be ludicrous to expect a child to sing a song or play an instrument without having a thorough grounding in music notation and theory. Playing and listening to music…are considered very advanced topics and generally put off till college, and more often graduate school.
As for the primary and secondary schools, their mission is to train students to use this language—to jiggle symbols around according to a fixed set of rules: “Music class is where we take out our staff paper, our teacher puts some notes on the board, and we copy them or transpose them into a different key…One time we had a chromatic scale problem and I did it right, but the teacher gave me no credit because I had the stems pointing the wrong way.”
…
Sadly, our present system of mathematics education is precisely this sort of nightmare.
So begins Paul Lockhart’s scathing critique of how mathematics is taught in this country, A Mathematician’s Lament. The book is an expansion of Lockhart’s essay of the same title. I encourage you to read the essay, buy the book, and share your thoughts in comments.
Yesterday we started a conversation about whether mathematics is invented or discovered. Today I’ll give you my three best arguments for “discovered”. And to focus the discussion, I’ll talk not about mathematics generally but about the natural numbers (0,1,2, and so forth) in particular.
I believe the natural numbers exist, quite independently of whether anyone’s around to think of them. Here’s why: First, we perceive them directly. Second, we know non-trivial facts about them. Third, they can explain the Universe. In more detail:
Continue reading ‘Real Numbers’
Is mathematics invented or discovered? In my experience, applied scientists often think of mathematics as a human invention, while actual mathematicians (with a few notable exceptions) feel sure that mathematics was always there to be discovered. (Of course, it’s sometimes hard to tell how much of this is genuine disagreement and how much is a language barrier.)
I’ve just finished reading an excellent book by Mario Livio which is entirely about the invention/discovery question, though he’s chosen the (somewhat unfortunate) title Is God a Mathematician? Much of the book is a lively romp through mathematical history, with a well chosen mix of biography and exposition. Although he parts company with them in the last chapter, Livio gives a more than fair hearing to the many great mathematicians who have insisted that they are discoverers, from Pythagoras through Galileo, G.H. Hardy, Kurt Godel, and the contemporary Fields Medalist Alain Connes (among others). Here, for example is Connes:
Continue reading ‘Jellyfish Math’
The Intelligent Design folk tell you that complexity requires a designer.
The Richard Dawkins crowd tell you that complexity must evolve from simplicity.
I claim they’re both wrong, because the natural numbers, together with the operations of arithmetic, are fantastically complex, but were neither created nor evolved.
I’ve made this argument multiple times, in The Big Questions, on this blog, and elsewhere. Today, I aim to explain a little more deeply why I say that the natural numbers are fantastically complex.
Continue reading ‘Non-Simple Arithmetic’
On his blog A Blank Slate, Vishal Patel posts a cute little brain teaser (with a hat tip to the Cosmic Variance blog):
Jack is looking at Anne, but Anne is looking at George. Jack is married, but George is not. Is a married person looking at an unmarried person?
(a) Yes
(b) No
(c) Can not be determined
This reminded me of one of my favorite little “zinger” math proofs. (If you think about the brain teaser long enough, you’ll see the connection.)
Continue reading ‘Rational Irrationality’
The mathematician John Baez has been dazzling science lovers on the web for over 15 years with his weekly Finds in Mathematical Physics. (He was a blogger long before there were blogs). Baez recently gave a lovely series of talks on his favorite numbers (they are 5, 8 and 24) in which he mentions Euler’s observation that if you sum up all the positive integers (1 + 2 + 3 + 4 + …) you get -1/12. (I promise, this is not a joke.)
Baez’s “proof” uses a little calculus, but I’ve reworked it into a form you can share with your middle schoolers—and better yet, have them share with their teachers.
Continue reading ‘A Little Arithmetic’
