Greg Mankiw, with a hat tip to his son Nicholas, asks for a plot of the function xx, where x is a real variable. The answer he points to (provided by Pedagoguery Software) gives this picture/expanation:
Continue reading ‘Humpty Dumpty’s Math Puzzle’
I’m eager to summarize the (largely excellent) discussion of last week’s nightmares and to talk about what it all means. I’ll surely get to that in the next few days. But meanwhile, we have another loose end to tie up.
I recently asked what comes next in the following series:
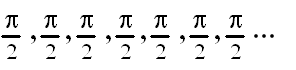
The answer, of course, is
Please raise your hand if you found this intuitively obvious.
In case your hand didn’t go up, consider the following sequence:
I continue to be bowled over daily by the high quality of the discussion at MathOverflow, and the prominence of many of the frequent participants. But this one was special:
A newbie poster asked for a pointer to a proof of the “de Rham-Weil” theorem. There’s a bit of ambiguity about what theorem this might refer to, but I had a pretty good of what the poster meant, so I responded that the earliest reference I know of is in Grothendieck‘s 1957 Tohoku paper — which led another poster to ask if this meant de Rham and Weil had had nothing to do with it.
This triggered an appearance from the legendary Roger Godement (had he been lurking all this time?), now aged 91 and one of the last survivors of the extraordinary circle of French mathematicians who rewrote the foundations of topology and geometry in the mid-20th century and changed the look, feel and content of mathematics forever. I tend to think of them as gods and demigods. Godement’s indispensable Theorie des Faisceaux was my constant companion in late graduate school. And now he has emerged from retirement for the express purpose of chastising me:
Continue reading ‘Touched by Greatness’
How secure is Internet security? A team of researchers recently set out to crack the security of about 6.6 million sites around the Internet that use a supposedly “unbreakable” cryptosystem. The good news is that they succeeded only .2% of the time. The bad — and rather shocking — news — is that .2% of 6.6 million is almost 13,000. That’s 13,000 sites with effectively no security. The interesting part is what went wrong. It’s a gaping security hole that I’d never stopped to consider, but is obvious once it’s pointed out.
Suppose you go around taking extremely close-up black-and-white pictures of randomly chosen natural and unnatural objects (rocks, trees, streams, buildings, etc.). What do they look like?
Well, each one looks like a patch of varying shades of gray, of course. But do some patches arise more than others? If each of your close-ups is, say, three pixels by three pixels, Which would you expect to see more of:
| This? |  |
Or this? |  |
Continue reading ‘Who Expected THAT?’
I don’t trust rocks. Rocks keep fooling me. They sit there looking all solid until you examine them more carefully and find out they’re mostly empty space, with a smattering of charged particles here and there. Then you look a little deeper and find out those charged particles are nothing like they first appeared. They don’t even have locations. Rocks, and their constituents, are nothing at all like they first present themselves. But at least they’re real. I think.
Now here’s what genuinely baffles me: Apparently there are people in this world (and even, occasionally, in the comments section of this blog) who haven’t the slightest doubt about the existence of rocks, galaxies, squirrels, and the rest of the physical universe, but who suddenly turn into hardcore skeptics re the existence of mathematical objects like the natural numbers. (Many of these people, I suspect, are in fact affecting skepticism because of a badly mistaken belief that it makes them look sophisticated. But that’s speculation on my part, so let’s put it aside and take their positions at face value.) I just don’t get this. Why on earth would, say, a scientist, commit to the belief that there’s a physical universe out there but not a mathematical one, when we know that our perceptions of the physical universe demand constant revision, whereas our perceptions of the mathematical universe are largely eternal. My conception of the natural numbers is very close to Euclid’s; my conception of an atom bears almost no resemblance to Demosthenes’s.
Back in the 1930’s, Kurt Godel proved two amazing facts about arithmetic: First, there are true statements in arithmetic that can’t be proven. Second, the consistency of arithmetic can’t be proven (at least not without recourse to logical methods that are on shakier ground than arithmetic itself).
Yesterday, I showed you Gregory Chaitin’s remarkably simple proof, of Godel’s first theorem. Today, I’ll show you Shira Kritchman and Ron Raz’s remarkably simple (and very recent) proof of Godel’s second theorem. If you work through this argument, you will, I think, have no trouble seeing how it was inspired by the paradox of the surprise examination.
Continue reading ‘The Big Surprise’
Today, I’m going to give you a short, simple proof of Godel’s First Incompleteness Theorem — the one that says there are true statements in arithmetic that can’t be proven. The proof is due to Gregory Chaitin, and it is far far simpler than Godel’s original proof. A bright high-schooler can grasp it instantly. And it’s wonderfully concrete. At the end, we’ll have an infinite list of statements, all easy to understand, and none of them provable — but almost all of them true (though we won’t know which ones).
Continue reading ‘Berry Interesting’
This is a tale of three paradoxes and why they matter.
The paradoxes are slippery, because they are stated in the imprecise language of English. But each of them has inspired a precise mathematical counterpart that is central to a brilliant argument in mathematical logic.
Continue reading ‘A Tale of Three Paradoxes’
If you’re the sort of person who reads this blog, you’re likely to be familiar with the paradox of the unexpected hanging, which has been floating around since 1943 but achieved popular notoriety around 1969 through the writing of Martin Gardner. But you’re less likely to be aware that the unexpected hanging plays a central role in a wonderful new piece of serious mathematics related to algorithmic complexity, Godel’s theorems, and the gap between truth and provability.
The unexpected hanging might as well be a surprise examination, and that’s the form in which I present this paradox to my students every year: In a class that meets every weekday morning, the professor announces that there will be an exam one day next week, but that students won’t know exactly which day until the exams are handed out.
The students, of course, immediately start trying to guess the day of the exam. One student (call him Bob) observes that the quiz can’t be on Friday — because if it is, the students will know that by Thursday afternoon. After all, if Monday, Tuesday, Wednesday and Thursday mornings have all passed by, only Friday remains. A Friday exam can’t be a surprise exam.
A more thoughtful student (call her Carol) observes that this means the quiz must be on one of Monday, Tuesday, Wednesday or Thursday — and that if it’s on Thursday, they’ll know that by Wednesday night. After all, Friday’s ruled out, so if Monday, Tuesday and Wednesday have passed by, then only Thursday remains. That rules out a surprise exam on Thursday.
Another student (call him Ted) observes that thanks to Bob and Carol, we know the exam must be on one of the first three days of the week — which means that if it’s not on Monday or Tuesday, it must be on Wednesday. Therefore if it’s on Wednesday, they’ll know this by Tuesday night. Scratch Wednesday from the list of possibilities.
Now Ted’s girlfriend Alice points out that the exam can’t be on Tuesday either. Whereupon Bob concludes that the exam must be on Monday. But wait a minute! Carol points out that if they know the exam will be on Monday, it can’t be a surprise. Therefore no surprise exam is possible.
The students, relieved, decide not to study. But they’re awfully surprised when they show up in class the following Tuesday and the professor hands out an exam.
Continue reading ‘The Surprise Exam, and More Surprises’
Today is the 200th birthday of Evariste Galois, who did not live to celebrate his 21st, but found time in his short 20 years to develop a circle of ideas that permeate modern mathematics. We know of these ideas because Galois spent the night of May 30, 1832 scribbling them furiously in a letter to a friend, in advance of the fatal duel he would fight the following morning. According to the great mathematician Hermann Weyl, “This letter, if judged by the novelty and profundity of ideas it contains, is perhaps the most substantial piece of writing in the whole literature of mankind.”
(If this were a less serious post, I might suggest that this famous letter was the first example of a Galois Correspondence.)
Now, two centuries later, every first year graduate student in mathematics spends a semester studying Galois Theory, and many devote their subsequent careers to its extensions and applications. Many of the greatest achievements of modern mathematics (for example, the solution to Fermat’s Last Theorem) are, at their core, elucidations of Galois’s 200-year-old insight.
Continue reading ‘Beauty, Truth and Symmetry’
Last week, the highly distinguished Princeton Professor Ed Nelson announced a proof that the Peano axioms for arithmetic are inconsistent — and hence so is arithmetic itself. If true, this would be much bigger news than faster-than-light neutrinos. It would be bigger news than a discovery that the South had won the American Civil War. It would be far, far bigger news than a discovery that all life on Earth was intelligently designed.
There are, after all, multiple proofs that Peano Arithmetic (that is, the fragment of arithmetic described by the Peano axioms) is consistent. Among those, the simplest and most convincing (to the overwhelming majority of mathematicians) is this: The axioms of Peano Arithmetic, and therefore the theorems of Peano Arithmetic, are all true statements about the natural numbers — and a set of true statements cannot contradict itself.
Ed Nelson rejects that argument because (exempting himself from that overwhelming majority) he doesn’t believe in the set of natural numbers — or perhaps even in individual numbers when those numbers are very large. (How do you know that 810000 exists? Have you ever counted to it?)
MathOverflow turns two years old this week — a milestone in the transformation of mathematical research into a massively collaborative endeavor. It’s happening on blogs, it’s happening on mailing lists, and it’s happening in a big way on MathOverlow, where mathematicians ask and answer the sorts of questions that might come up in the faculty lounge — if the faculty lounge were populated by hundreds of experts pooling their expertise.
If you’re interested in mathematics at the research level, MathOverflow is a place to learn something new and fascinating every single day. (If you are not doing mathematics at a research level, feel free to read but please don’t feel free to join the fray; questions at anything below about a second-year graduate level should be directed to MathStackExchange, another massively collaborative site aimed, roughly, at the college level — which reminds me that it’s not just mathematical research, but also mathematical education, that is being revolutionized before our eyes.)
Continue reading ‘Happy Birthday’
The game of Cats and Dogs works like this: You and your teammate are placed in separate rooms and forbidden to communicate. You are each asked a randomly chosen question: Either “Do you like cats?” or “Do you like dogs?” (Each of your questions is determined by a separate fair coin flip.)
You win if your answers agree — unless you were both asked the “cats” question, in which case you win if your answers disagree.
A little reflection should convince you that if you are allowed to meet with your partner and plot strategy before the game, then the best you can do is agree to always agree — say by both always answering “yes”. That way, you win 75% of the time, and there’s no way to do better. In particular, there’s nothing to be gained by randomizing your answers.
That, at least, is true, in a world governed by the laws of classical physics and probability theory. But in a world governed by the laws of quantum mechanics — which is to say, in the world we live in — you can in principle do better. Namely: You each carry with you one of a pair of entangled “quantum coins” (actually elementary particles, but I prefer to think of them as coins, since you’re going to use them as randomizing devices).
Continue reading ‘Cats, Dogs and Quantum Mechanics’
Re yesterday’s puzzle, you’ll find answers in the comments. (We are blessed with some very smart commenters here at The Big Questions!!)
Commenter Roger Schlafly pointed this Wikipedia article where I was surprised and delighted to see a reference to a paper co-written by my old friend Dave Rusin. I did not remember that Dave had anything to do with this problem, but in retrospect I bet I knew this at one time.
I managed to dig out some notes I jotted down on this subject many many years ago. I have not doublechecked these results, and I can’t completely vouch for the careful accuracy of my younger self, so take these for what they’re worth. But here’s what I once claimed to have proved:
The reason there is exactly one pair of nonstandard six-sided dice is that six is the product of two distinct primes. For the same reason, there is exactly one pair of nonstandard n-sided dice when n is 10, or 15, or 21, or …. For any product of three distinct primes, there are at most 40 nonstandard pairs.
I also found (in what appears to be my handwriting) this chart, which I reproduce with the same caveats:
Continue reading ‘Friday Solution’
I love this problem, which I found on the Internet many years ago. I suppose you could find a solution by Googling, but that’s of course no fair.
A standard pair of six-sided dice induce a probability distribution on the outcomes 1 through 12: The probability of rolling a 1 is 0, of rolling a 2 is 1/36, of rolling a 3 is 1/18, etc. Is there any nonstandard pair of six-sided dice that induces exactly the same probability distribution? If so, how many such pairs are there?
(A non-standard pair of six-sided dice might have, say, the numbers 1,2,2,3,8,9 on one cube and the numbers 2,3,4,4,4,4 on the other.)
Continue reading ‘Thursday Puzzle’
The most fun you can have on the Internet is to find a beautiful, succinct argument with a conclusion so unexpected it seems like magic. For today’s fun, I am indebted to Michael Lugo, at God Plays Dice.
Lugo’s original post is so good it seems almost superflous to paraphrase it, but I can’t resist the temptation.
Drill a tunnel through the earth, from anywhere to anywhere — New York to Maine, or New York to Australia, or wherever else you like. Like so:
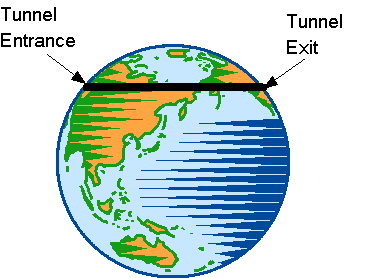
Now drop the object of your choice (Lugo suggests a burrito, but you might prefer a gravity-driven train) into the tunnel entrance and wait till it comes out the other side. It’s a standard calculus problem to calculate how long you’ll have to wait: The answer is 42 minutes, regardless of the length of the tunnel. I’m sure I once found it surprising that the tunnel length doesn’t matter, but I’ve known it long enough that I now take it in stride. So that’s not how Lugo surprised me.
The surprise is that if you change the size of the earth (while maintaining its density), the answer is still 42 minutes. Whether the earth is the size of a pea or the size of the solar system, it’s a 42 minute trip from one end of the tunnel to the other. (We’re — quite reasonably — ignoring the effects of relativity here. For an earth that was half the size of the universe, we’d have to make some corrections.)
Why so? You could, of course, discover this through a direct calculation. But Lugo provides a much slicker argument, namely:
Continue reading ‘Tunnel Vision’
Vladimir Voevodsky, one of the world’s best and most influential mathematicians, has stirred up a bit of a hornet’s nest with a video lecture suggesting the possibility that the Peano Axioms — the standard axioms for arithmetic — might be inconsistent.
Since the Peano Axioms are known to be consistent, it’s tempting to dismiss the whole lecture as either a prank or a shocking display of ignorance. The latter temptation is buttressed somewhat by Voevodsky’s bold misstatement of Godel’s Incompleteness Theorem, which plays a central role in the lecture. On the other hand, Voevodsky is smarter than almost anyone else on earth, which earns him the benefit of the doubt — maybe what he’s saying is subtler than it seems. On the other hand, some of those in the “shocking display of ignorance” camp are among the few people in the world who might be as smart as Voevodsky.
To believe that the Peano Axioms are inconsistent, Voevodsky must reject all of the known proofs that they are consistent. In particular, he must reject the simplest and most convincing of all those proofs, which goes like this:
Continue reading ‘Inconsistency’
Through the 1970s — which is to say, yesterday — Dan Quillen barraged the field of algebraic topology with a stream of new techniques and concepts that not only invigorated the field, but ramped up its power to solve problems in geometry, arithmetic and other mathematical areas where you might have thought topology had no business sticking its nose.
The greatest of these great accomplishments was Quillen’s development of higher algebraic K-theory, a long-sought holy grail for mathematicians. Pre-Quillen, one had a sense that there ought to be a subject called higher K-theory, and a general sense of what it should look like, and reasons to hope that K-theory, if only we could figure out what it was, would be the great unifying theme behind much of mathematics, and a tool for translating insights in one field into useful techniques in another. Many had tried and failed to lay the foundations of the subject. Then Quillen, in one 63 page paper, not only laid the foundations but brought the subject to a state of maturity that, in the words of Hyman Bass, one normally expects from the efforts of several mathematicians over several years:
The paper…is essentially without mathematical precursors. Reading it for the first time is like landing on a new and friendly mathematical planet. One meets there not only new theorems and new methods, but new mathematical creatures and a complete paradigm of gestures for dealing with them.
Much of my mathematical youth was spent exploring that planet. I met Quillen only once, and very briefly, but great mathematicians, like great poets, reveal so much of themselves in their work that one comes to feel a certain intimacy just by studying them. In that sense, Quillen was my close companion many a year.
Dan Quillen died this week at the age of 70, after a five year battle with Alzheimer’s. Scouring the web for obituaries and other recent mentions, I found very little besides a brief article from a Gainesville newspaper about an Alzheimer’s patient named Daniel Gray Quillen who had gone briefly missing in June, 2010. Followup stories identify the missing man as “a senior citizen with Alzheimer’s”.
“A senior citizen”?!?!?! Part of me wants to scream: “Dammit, this is no generic senior citizen! This is Daniel Fucking Quillen, Fields Medalist, Cole Prize Winner, architect of higher K-theory, conqueror of the Serre conjecture, and one of the intellectual giants of the 20th century!”
Arguably none of that has any place in a short note about a man gone briefly missing, so my gripe is not with the Gainesville Sun. My gripe is with the Universe. If I were running the Universe, there’d be some level of accomplishment that confers immunity from death, deterioration and obscurity. I’m not sure exactly where I’d set that bar, but I’m sure Dan Quillen would have cleared it.
This is really very cool. In several ways.
First: For the past year or so, there has been a remarkable website called Math Overflow where research mathematicians gather to swap ideas, to ask for help when they get stuck, and to offer help when they can. Frequent contributors include the Fields Medalists (a Fields Medal is roughly the mathematical equivalent of a Nobel Prize) Terry Tao, Tim Gowers, Bill Thurston and Richard Borcherds. Others who have popped up from time to time include Vaughan Jones (yet another Fields Medalist), John Tate, whose thesis reshaped modern number theory, and Peter Shor, the pioneering figure in quantum computation. And every day, one runs across dozens of other folks who nearly any top math department would be proud to have (and in many cases are proud to have) on their faculties. If you already know a lot of math, you can get a hell of an advanced education browsing this site.
Today is the birthday of the magnificent Emmy Noether, known as the “mother of modern algebra”, and one of my mathematical heroes. She is one of the few mathematicians in history who fundamentally changed what mathematics is about.
It was Emmy (I use her first name in order to distinguish her from her mathematician father Max) who first fully recognized the power of abstraction, which became the driving force of 20th century mathematics. She demonstrated time and again that it can be easier to solve a general problem than a specific one, and therefore the best way to attack a specific problem is often to generalize. Do you want to prove a fact about polynomial functions? First notice that polynomial functions can be added together, and they can be multiplied, and they obey certain laws along the way (like associativity and commutativity). Now prove a theorem that applies to anything that can be added and multiplied subject to those laws. Do it right, and you’ll replace intricate calculations with simple logical deductions. What was hard becomes easy. You get your result for free, and a whole lot of other results as a bonus.
Or, if you that doesn’t quite work, figure out what additional properties you’re using about polynomials, beyond associativity and commutativity, and prove a theorem about everything that has those properties.
To get a sense of how revolutionary this was, consider the Hilbert Basis Theorem, one of the foundational results of modern algebra. Have a look at Hilbert’s original proof — though you might not want to work through every detail in the 62 pages of equations and formulas. By contrast, Noether’s proof of a more general, more powerful and more useful version occupies all of one paragraph on Wikipedia.
Continue reading ‘The Art of Abstraction’
Sorry to have been uncharacteristically absent all week; I’ve been busy in a good way, though I hope and expect to get back to more regular blogging before long. In the meantime, to keep you busy, let me give you a pointer to a marvelous essay I’ve long been a fan of, and just happened to get reminded of today: Scott Aaronson’s take on the old riddle of who can name the biggest number. Have fun with this, and I’ll see you soon.
It has been said of Lubos Motl that he’s hard to ignore, but it’s always worth the effort. I will, soon enough, take this advice to heart. But not quite yet. Lubos’s penchant for twisting other people’s words, just so he can have something to argue about, is well known and widely remarked. As his most recent victim (though “victim” is of course too strong a word, no actual harm having been done), I thought it would be both fun and instructive to challenge him to a bet. True to form, he continued to bluster but of course refused to back up his misrepresentations with actual cash.
Now of course Lubos will say that it is I who am twisting words, and in particular that I either “changed the question” or “changed the answer” (or both) between the original post and the offer to bet. That, however, won’t wash, since I’ve agreed, as part of the terms of the bet, to let an impartial panel of statistics professors determine the answer to the question as it was originally posed. So even if I had changed the question (which I haven’t), this would prevent me from getting away with it. (And no, I haven’t changed the answer either. If Lubos claims I have, we can put that to the stats profs also.)
I’m feeling annoyed enough to say a little more along these lines, but first I’d like to make it crystal clear that my annoyance does not extend to readers who are still puzzling this out. The problem with Lubos isn’t that he’s got it wrong; it’s that he’s not the least bit interested in getting it right. A few particulars:
Continue reading ‘Slippery Lube’
Bertrand Russell, that most rational of men, was nonetheless plagued by intermittent depression and the occasional nightmare. Including this one, as reported by Russell’s confidante, the mathematician G.H. Hardy:
[Russell] was in the top floor of the University Library, about A.D. 2100. A library assistant was going round the shelves carrying an enormous bucket, taking down books, glancing at them, restoring them to the shelves or dumping them into the bucket. At last he came to three large volumes which Russell could recognize as the last surviving copy of Principia Mathematica. He took down one of the volumes, turned over a few pages, seemed puzzled for a moment by the curious symbolism, closed the volume, balanced it in his hand and hesitated….
Principia Mathematica, to which Russell had devoted ten years of his life, was his (and co-author Alfred North Whitehead‘s) audacious and ultimately futile attempt to reduce all of mathematics to pure logic. It is a failure that enabled some of the great successes of 20th century mathematics. And — the first volume having been published in December, 1910 — this is its 100th birthday.
Continue reading ‘Lord Russell’s Nightmare’
Today I want to tell you about the single most counterintuitive-but-true thing I’ve ever heard.
Suppose you’re observing something that changes over time — say the Dow Jones average, or the temperature in Barrow, Alaska, or the number of people who have been shot by terrorists so far this year. Suppose you have absolutely no prior information about how this thing behaves — in particular, you might have no way of knowing whether it changes continuously (like the temperature) or whether it’s subject to sudden changes (like the number of terrorist victims). You have no formula for it; you don’t even know whether there is a formula. It could be absolutely anything.
Continue reading ‘The Most Counterintuitive Theorem EVER’
 |
God created the integers. All else is the work of man. —Leopold Kronecker |
The problem with knowledge is that you have to start somewhere. Once you know something, you can start deducing other things. But how do you know the first thing?
Descartes’s famous solution was “I think, therefore I am”. I have direct knowledge of my own thoughts, and this in turn tells me that I exist. Now we can go on.
Mathematics, like all other knowledge, needs a starting point. Most of our mathematical knowledge is deduced from prior mathematical knowledge. I know that every positive integer is the sum of four squares because I know how to deduce this fact from other things I know. But where do I start?
There seems to be a widespread misconception (widespread, that is, among non-mathematicians — mathematicians know better) that all we know is what we can derive from axioms. This is wrong for several reasons. Two of these I’ve blogged about repeatedly in the past (e.g. here, here, and here and here), but the third is even more fundamental:
Continue reading ‘First Things’
This weekend marked the 80th anniversary of the most significant event in the history of logic since the days of Aristotle. On October 23, 1930, the 24-year-old Kurt Godel presented his incompleteness theorems to the Vienna Academy of Sciences.
The first incompleteness theorem says this: No matter what axioms you start with, there will always be statements in arithmetic that you can neither prove nor disprove. (I am glossing over some technicalities here, but in this context they are not important.) Some of those statements take the form “Such-and-such an equation has (or does not have) any solutions”. You tell me your axioms, and I’ll produce an equation that you can neither prove solvable nor prove insolvable.
Continue reading ‘Eighty Years of Incompleteness’
About a year ago, when I was a novice blogger, I posted a piece called “A Little Arithmetic”. The arithmetic all looked fine in my browser, but I failed to realize that it might not look fine in everyone’s. As a result, some of you found it unreadable. But I like to think it was worth reading, so now that I’ve figured out how to make it look nice, I’m posting it again:
The mathematician John Baez has been dazzling science lovers on the web for over 15 years with his weekly Finds in Mathematical Physics. (He was a blogger long before there were blogs). Baez recently gave a lovely series of talks on his favorite numbers (they are 5, 8 and 24) in which he mentions Euler’s observation that if you sum up all the positive integers (1 + 2 + 3 + 4 + …) you get -1/12. (I promise, this is not a joke.)
Baez’s “proof” uses a little calculus, but I’ve reworked it into a form you can share with your middle schoolers—and better yet, have them share with their teachers.
Continue reading ‘A Little Arithmetic’
Some quick words about the mathematical universe, which is the theme of the first chapter of The Big Questions:
1. A “mathematical object” consists of abstract entities (that is, “things” with no intrinsic properties) together with some relations among them. For example, the euclidean plane that you studied in high school geometry consists of points, together with certain relations among them (such as “points A, B and C are collinear”). Mathematical objects can be very complicated. Mathematical objects can have “substructures”, which is a fancy name for “parts”. A line in the plane, for example, is a substructure of the plane.
2. Every modern theory of physics says that our universe is a mathematical object, and that we are substructures of that object. Theories differ only with regard to which mathematical object we happen to be a part of. Particles, forces and energy are not just described by equations; they are the equations (together with abstract, purely mathematical relations among those equations).
Continue reading ‘The Mathematical Universe’
