Archive for the 'Heroes' Category
The poster to the left hangs on the wall of my office. Can you figure out the pattern to the sequence? Now can you estimate the size of the nth entry?
John Horton Conway died yesterday, a victim of Covid-19. His unique mathematical style combined brilliance and playfulness in equal measure. I came across his “soldier problem” at an impressionable age, and was astonished by the beauty of the solution. You’ve got an infinite sheet of graph paper, with one horizontal grid line marked as the boundary between friendly and enemy territory. You can place as many soldiers as you like in friendly territory, at most one to a square. Now you can start jumping your soldiers over each other — a soldier jumps horizontally or vertically, over an adjacent soldier (who is then removed from the board) into an empty square. The goal is to advance at least one soldier to the fifth row of enemy territory. Conway’s proof that it can’t be done struck me then as utterly beautiful, utterly unexpected, and a compelling reason to learn more about this mathematics business.
He invented the Game of Life. He invented the system of surreal numbers, a vast generalization of the usual real numbers, designed for the purpose of assigning values to positions in games but adopted by mathematicians for purposes well beyond its original design. (Don Knuth’s book on the subject is a classic, and easy reading). His Monstrous Moonshine conjecture is the reason I own a t-shirt that says:
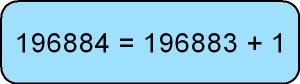
which I am prepared to argue is the most remarkable equation in all of mathematics. He was the first person to prove that every natural number is the sum of 37 fifth-powers. More than a century after mathematicians first gave a complete classification of two-dimensional surfaces, Conway (together with George K. Francis) found a much better proof. He worked in geometry, analysis, algebra, number theory and physics. And reportedly, he could solve a Rubik’s Cube behind his back, after inspecting it for a few seconds.
Gone now, along with John Prine — another icon of my youth — and too many others. I got the word about Conway just as I was about to go to bed, and am typing this in a state of exhaustion. If I were more awake, it would be more coherent, but it will have to do.
Congratulations to the winners of this morning’s exceptionally well-deserved Nobel Prize.
Time is scarce, and lately I’ve been devoting it mostly to things other than blogging — but I feel the need to emerge from hiding just long enough to acknowledge the shocking death today of the extraordinary mathematician Vladimir Voevodsky at the age of 51.
Voevodsky is best known for finding the right definition of motivic cohomology sometime around the year 2000. This was a Holy Grail, the quest for which had been set in motion by the earth-shattering vision of Alexander Grothendieck. I happen to have been leafing through my well-worn copy of Voevodsky’s book on Cycles, Transfers and Motivic Homology Theories (co-written with Andrei Suslin and Eric Friedlander) when I heard of his death.
More recently, Voevodsky had turned his attention to logic and the foundations of mathematics. Here is video of his talk “What if the Current Foundations of Mathematics Are Inconsistent?”
A brief obituary is here. A brief mathematical autobiography, written by Voevodsky, is here. I might return and add a few personal reminscences.
The most exciting news of the past week had nothing to do with James Comey or Donald Trump.
The University of Montpelier has released high-quality scans of about 18,000 pages of notes and scribbles by Alexandre Grothendieck. If you’re competent in both French and the art of deciphering handwriting that was never meant to be readable except to the author, you can while away some hours sifting through them here.
It would be an understatement to say that Grothendieck was never shy about revealing and publicly analyzing his thought processes, but these notes are presumably less filtered than the tens of thousands of pages he chose to share in his lifetime. FOr the many who are already sifting through them, and for the many more who are waiting to hear the reports of the sifters, they will yield new insights into one of the most extraordinary minds in human history.
For an upcoming Festschrift, I was recently asked to write an account of Dee (then Don) McCloskey‘s years as a brilliant teacher at the University of Chicago, her influence on a generation of economists, and my own enormous debts to her. This was a great pleasure to write. A draft is here.
Paul A.M. Dirac was a pioneer of quantum mechanics and quantum field theory. His work pervades all of modern physics. He was, by almost all accounts, one of the top 10 physicists of all time, and by many accounts one of the top 2 physicists of the 20th century. And he’s one of my personal heroes.
When Dirac was awarded the Nobel prize in 1933, he was asked to say a few words at the banquet that kicks off the multi-day Nobel celebration — and chose, against tradition, to speak about a subject other than physics. Here is Paul Dirac on the source of all our economic problems:
I should like to suggest to you that the cause of all the economic troubles is that we have an economic system which tries to maintain an equality of value between two things, which it would be better to recognise from the beginning as of unequal value. These two things are the receipt of a certain single payment (say 100 crowns) and the receipt of a regular income (say 3 crowns a year) through all eternity. The course of events is continually showing that the second of these is more highly valued than the first. The shortage of buyers, which the world is suffering from, is readily understood, not as due to people not wishing to obtain possession of goods, but as people being unwilling to part with something which might earn a regular income in exchange for those goods. May I ask you to trace out for yourselves how all the obscurities become clear, if one assumes from the beginning that a regular income is worth incomparably more, in fact infinitely more, in the mathematical sense, than any single payment? In doing so I think you would then get a better insight into the way in which a physical theory is fitted in with the facts than you could get from studying popular books on physics.
True to form, then, Dirac set an agenda that others scurried to follow — the agenda in this case being the exploitation of the Nobel prize as a license to spout economic gibberish. Almost a century later, his program continues to flourish.
I never met Alexander Grothendieck. I was never in the same room with him. I never even saw him from a distance. But whenever I think about math — which is to say, pretty much every day — I feel him hovering over my shoulder. I’ve strived to read the mind of Grothendieck as others strive to read the mind of God.
Those who did know him tend to describe him as a man of indescribable charisma, with a Christ-like ability to inspire followers. I’ve heard it said that when Grothendieck walked into a room, you might have had no idea who he was or what he did, but you definitely knew you wanted to devote your life to him.
And people did. In 1958, when Grothendieck (aged 30) announced a massive program to rewrite the foundations of geometry, he assembled a coterie of brilliant followers and conducted a seminar that met 10 hours a day, 5 days a week, for over a decade. Grothendieck talked; others took notes, went home, filled in details, expanded on his ideas, wrote final drafts, and returned the next day for more. Jean Dieudonne, a mathematician of quite considerable prominence in his own right, subjugated himself entirely to the project and was at his desk every morning at 5AM so that he could do three hours of editing before Grothendieck arrived and started talking again at 8:00. (Here and elsewhere I am reporting history as I’ve heard it from the participants and others who followed developments closely as they were happening. If I’ve got some details wrong, I’m happy to be corrected.) The resulting volumes filled almost 10,000 pages and rocked the mathematical world. (You can see some of those pages here).
I want to try to give something of the flavor of the revolution that unfolded in that room, and I want to do it for an audience with little mathematical background. This might require stretching some analogies almost to the breaking point. I’ll try to be as honest as I can. In the first part, I’ll talk about Grothendieck’s radical approach to mathematics generally; after that, I’ll talk (in a necessarily vague way) about some of his most radical and important ideas.
Continue reading ‘The Generalist’
Around 1970, Alexander Grothendieck, the greatest of all modern mathematicians and arguably the greatest mathematician of all time, announced — at the age of 42 — the official end of his research career. Another great mathematician once told me that he thought he knew why. Following two decades of discoveries and insights that, one after the other, stunned the mathematical world, Grothendieck had, for the first time, achieved an insight so unexpected and so consequential that he himself was stunned. Grothendieck had discovered his own mortality.
I am told that just a few hours ago, his vision proved accurate. But the notion of Grothendieck as a mortal seems hard to swallow. He dominated pure mathematics not just through the force of his ideas — ideas that seemed eons ahead of everyone else’s — but through the force of his personality. When, around 1960, he announced his audacious plan to solve the notoriously difficult Weil conjectures by first rewriting the foundations of geometry, dozens of superb mathematicians put the rest of their careers on hold to do their parts. The project’s final page count, including the twelve volumes known as SGA (Seminaire de Geometrie Algebrique) and the eight known as EGA (Elements de Geometrie Algebrique) approached 10,000 pages. The force and clarity of Grothendieck’s unique vision scream forth from nearly every one of those pages, demanding that the reader see the mathematical world in a new and completely original way — a perspective that has proved not just compelling, but unspeakably powerful.
In Grothendieck, modesty would have been ridiculous, and he was never ridiculous. Here, in his own words — words that ring utterly true — is Grothendieck’s own assessment of how he stood apart (translated from French by Roy Lisker):
Most mathematicians take refuge within a specific conceptual framework, in a “Universe” which seemingly has been fixed for all time – basically the one they encountered “ready-made” at the time when they did their studies. They may be compared to the heirs of a beautiful and capacious mansion in which all the installations and interior decorating have already been done, with its living-rooms , its kitchens, its studios, its cookery and cutlery, with everything in short, one needs to make or cook whatever one wishes. How this mansion has been constructed, laboriously over generations, and how and why this or that tool has been invented (as opposed to others which were not), why the rooms are disposed in just this fashion and not another – these are the kinds of questions which the heirs don’t dream of asking . It’s their “Universe”, it’s been given once and for all! It impresses one by virtue of its greatness, (even though one rarely makes the tour of all the rooms) yet at the same time by its familiarity, and, above all, with its immutability.
One hundred years ago today, in a back room on the second floor of a middle class row home in the Welsh city of Swansea, Dylan Thomas issued his first demand for the world’s attention. His cries, I feel sure, struck onlookers as both profoundly expressive and infuriatingly difficult to understand. It was a schtick he spent 39 years refining.
I believe that Thomas at his best was the finest lyric poet ever to write in English, and at his worst a pretentious windbag. The best is more than ample compensation for the worst. At age 12, he won a prize for a poem he’d submitted to a children’s magazine, and as an adult he kept a copy of that poem, cut from the magazine, pasted to his bathroom mirror. Only after he died did some literary detective discover that Thomas had plagiarized the poem. But before he was out of his teens, he wrote the superb and brilliantly original “I See the Boys of Summer”, which I am quite sure nobody else could have conceived or executed.
Because this is Thomas’s birthday, and because every blogger is entitled to an occasional bit of self-indulgence (how else could you explain Bob Murphy’s karaoke posts?), I present here a recital of the best of Thomas’s several birthday poems. For balance, you’ll find below the cut a recital of Thomas’s finest death poem (no, it’s not “Do Not Go Gentle”), and two more of my favorites on the recurrent Thomas themes of birth and the passage of time.
(Related: My 90th/96th birthday appreciation.)
Get the Flash Player to see this content.
(If you have a problem with the flash video, try clicking here — or right-click to download and save.)
Continue reading ‘Blogpost in October: 100 Years to Heaven’
Fifty years ago this Labor Day weekend, the presidential campaign of 1964 got underway in earnest. It is often said that Barry Goldwater “lost the election but won the Republican party” or even “lost the election but won the future” by nudging the center of either the party or the country several notches to the right.
I don’t see it. Where is the contemporary mainstream politician — Republican or otherwise — who would repeal the 1964 Civil Rights Act, or at least those provisions (Titles II and VII) that authorize Federal regulators to override private business decisions about whom to serve and whom to hire? Where is the contemporary mainstream politician who would sell the Tennessee Valley Authority? Or end all agricultural supports? If Goldwaterism is in fact ascendant, then how did entitlement spending, as a percentage of GDP, manage to grow for most of the past 20 years — even though Republicans controlled the House of Representatives for 16 of those 20? For that matter, how is it that after all those years of Republican control, the National Endowments of the Arts and Humanities — two of the more noxious weeds to arise from the soil of the Goldwater defeat — continue to thrive?
Continue reading ‘The Goldwater Standard’
A long time ago, when I had just started teaching at the University of Rochester, a blind man marched into my office, adopted a commanding stance, and announced in a booming voice that “it takes 150 condoms to prevent one birth in India”. Then he turned on his heels and marched out, leaving me to wonder what he had divided into what to get that number.
That’s what it was like working with Walter Oi, who died peacefully in his sleep on Christmas Eve after a long illness. Walter loved odd facts, and he loved to share them. It was Walter who told me that when all frozen pies had 12 inch diameters, apple was the most popular flavor — but when 7 inch pies came on the market, apple immediately fell to something like fifth place. His explanation: When you’re buying a 12 inch pie, the whole family has to agree on a flavor, and apple wins because it’s everyone’s second choice. With 7 inch pies, family members each get their pick, and almost nobody chooses apple.
Walter loved facts so much that he sometimes invented new ones, because the world could always use more. One day he walked into the department coffee room and announced that “A one hundred pound man and a three hundred pound man have exactly the same quantity of blood.” When this was met with considerable skepticism, Walter responded as he always responded to skepticism — by repeating himself more forcefully: “A one hundred pound man and a three hundred pound man have EXACTLY the same quantity of blood”.
In those pre-Internet days, some of us owned a device called an “encyclopedia”, which was sort of like a hardcopy printout of Wikipedia, but with fewer Simpsons references. A couple of my more enterprising colleagues went home and checked their encyclopedias that night, and came back the next morning to report that according to authoritative sources, a man’s blood volume is roughly proportional to his body weight. Walter’s response: “Nope. A one hundred pound man and a three hundred pound man have EXACTLY the same quantity of blood.”
If you watched carefully and didn’t blink, you might have caught him suppressing a smile.
Continue reading ‘Walter Oi, 1929 – 2013’
Ronald Coase has died at the age of 102. I am therefore reposting, with minor changes, the appreciation I wrote a few years ago for his 99th birthday.
In the theory of externalities—that is, costs imposed involuntarily on others—there have been exactly two great ideas. The first, forever associated with the name of Arthur Cecil Pigou (writing about 1920) is that things tend to go badly when people can escape the costs of their own behavior. Factories pollute too much because someone other than the factory owner has to breathe the polluted air. Nineteenth century trains threw off sparks that tended to ignite the crops on neighboring farms, and the railroads ran too many of those trains because the crops belonged to someone else. Farmers keep too many unfenced rabbits when they don’t care about the lettuce farmer next door.
Pigou’s solution—and it’s often a good one—is to make sure that people do feel the costs of their actions, via taxes, fines, or liability rules that allow the victims to sue for damages. Do a dollar’s worth of damage, and you’re charged a dollar.
Pigou endorsed this policy not because it seems fair, though it does seem fair to many, but because it yields, under what he believed to be very general conditions, the optimal amounts of damage. We don’t want too much pollution, but we don’t want too little, either, given that pollution is a necessary by-product of a lot of stuff we enjoy. Pigou offered a proof—now standard fare in all the textbooks—that his policies lead to the perfect compromises, in a sense that can be made precise.
The second great idea about externalities sprang full-blown from the mind of a law professor and subsequent Nobel prize winner named Ronald Coase, who stunned the profession in 1960 by pointing out that Pigou’s argument runs both ways. If you breathe the pollution from my factory, I’m imposing a cost on you—but at the same time, you’re imposing a cost on me. After all, if you lived somewhere else, you wouldn’t be complaining about the smoke and I wouldn’t be getting punished for it.
Continue reading ‘RIP, Ronald Coase’
I mentioned earlier this week that I’d been crafting a long post on the fabric of the Universe when I was sidetracked by relatively mundane political events. Now I’ve been sidetracked again by the entirely unexpected (to me) news of the death from melanoma, at age 65, of the Fields Medalist Bill Thurston, who devoted his life to understanding the shape of space.
One-dimensional topology is the study of curves and two-dimensional topology is the study of surfaces. Both subjects are quite well understood. Thurston was the king of three-dimensional topology, which gains additional interest from the fact that we perceive ourselves as living in a three-dimensional Universe. Three-dimensional topology attempts to classify all the possible shapes for that Universe.
One of course is also interested in four, five, six and many-dimensional topology, four dimensions being of particular interest because they can be used to model space together with time. But although three dimensions are more complicated than two and two are more complicated than one, it turns out that when you go much higher, a lot of things get simpler. Consider knots, for example. There are no knots inside a one or two dimensional space; a knot needs three dimensions in which to pass over and under itself. But in more than three dimensions, you can untie any knot just by pulling on its ends — roughly because the additional dimensions give it so much space in which to untangle itself. For those and related reasons, topology is often hardest in three and four dimensions — coincidentally (or maybe not) the very dimensions most relevant to the way we experience the world.
Thurston revolutionized three-dimensional topology in the 1980s with his geometrization conjecture, which says that any three-manifold (the three-dimensional analogue of a smooth curve or surface) can be cut up into pieces, each of which exhibits one of eight permissible geometries. The simplest of those geometries is the flat three-dimensional space you think you see around you, where you can draw three straight lines in mutually perpendicular directions and extend them forever. Another is the geometry of the three-dimensional sphere, which is an analogue of the two-dimensional surface of the earth, where any “straight” line eventually circles back to meet itself.
The geometrization conjecture was important, but what really mattered was the vast array of new techniques Thurston introduced for visualizing and understanding the structure of three-manifolds. When those techniques came on line in the early 1980s, he was widely acclaimed as the mathematician of the decade.
One thing that set Thurston apart was his insistence that mathematics is a human study, and that it’s the mathematician’s job to communicate not just theorems and proofs, but a unique way of thinking. Stories are often told of mid-twentieth century mathematicians (usually French) who, when asked a question about their work, would scribble a picture on the blackboard, deliberately stand in front of that picture to shield it from everyone else’s view, and then, having studied it a few minutes, erased the picture, turned around, and gave a purely formal explanation designed to obscure all of the motivation and insight. Nobody ever told a story like that about Bill Thurston. Here he is, talking about the mystery of three-manifolds; dip in at a random moment and chances are excellent you’ll hear him talking not about how he proved a theorem but about how he sees the world:
Continue reading ‘The Visionary’
I continue to be bowled over daily by the high quality of the discussion at MathOverflow, and the prominence of many of the frequent participants. But this one was special:
A newbie poster asked for a pointer to a proof of the “de Rham-Weil” theorem. There’s a bit of ambiguity about what theorem this might refer to, but I had a pretty good of what the poster meant, so I responded that the earliest reference I know of is in Grothendieck‘s 1957 Tohoku paper — which led another poster to ask if this meant de Rham and Weil had had nothing to do with it.
This triggered an appearance from the legendary Roger Godement (had he been lurking all this time?), now aged 91 and one of the last survivors of the extraordinary circle of French mathematicians who rewrote the foundations of topology and geometry in the mid-20th century and changed the look, feel and content of mathematics forever. I tend to think of them as gods and demigods. Godement’s indispensable Theorie des Faisceaux was my constant companion in late graduate school. And now he has emerged from retirement for the express purpose of chastising me:
Continue reading ‘Touched by Greatness’
On May 17 of this year, these fifteen World War II veterans were awarded the French Legion of Honor medal for their service in France. They were cited for their courage and their contributions toward the French liberation. Third from the left, in the light blue jacket, is my Dad.
Words like “awe” and “gratitude” cannot begin to describe what I feel toward these people, whose sacrifices secured the unprecedented safety, prosperity and freedom that have graced my life and so many others of my generation. In the world they created, those sacrifices have become (for people like me) unimaginable.
These are the giants who cleared my path through life. I’m glad to see them honored, though no honor can ever be enough.
Continue reading ‘The Honor Roll’
Through the 1970s — which is to say, yesterday — Dan Quillen barraged the field of algebraic topology with a stream of new techniques and concepts that not only invigorated the field, but ramped up its power to solve problems in geometry, arithmetic and other mathematical areas where you might have thought topology had no business sticking its nose.
The greatest of these great accomplishments was Quillen’s development of higher algebraic K-theory, a long-sought holy grail for mathematicians. Pre-Quillen, one had a sense that there ought to be a subject called higher K-theory, and a general sense of what it should look like, and reasons to hope that K-theory, if only we could figure out what it was, would be the great unifying theme behind much of mathematics, and a tool for translating insights in one field into useful techniques in another. Many had tried and failed to lay the foundations of the subject. Then Quillen, in one 63 page paper, not only laid the foundations but brought the subject to a state of maturity that, in the words of Hyman Bass, one normally expects from the efforts of several mathematicians over several years:
The paper…is essentially without mathematical precursors. Reading it for the first time is like landing on a new and friendly mathematical planet. One meets there not only new theorems and new methods, but new mathematical creatures and a complete paradigm of gestures for dealing with them.
Much of my mathematical youth was spent exploring that planet. I met Quillen only once, and very briefly, but great mathematicians, like great poets, reveal so much of themselves in their work that one comes to feel a certain intimacy just by studying them. In that sense, Quillen was my close companion many a year.
Dan Quillen died this week at the age of 70, after a five year battle with Alzheimer’s. Scouring the web for obituaries and other recent mentions, I found very little besides a brief article from a Gainesville newspaper about an Alzheimer’s patient named Daniel Gray Quillen who had gone briefly missing in June, 2010. Followup stories identify the missing man as “a senior citizen with Alzheimer’s”.
“A senior citizen”?!?!?! Part of me wants to scream: “Dammit, this is no generic senior citizen! This is Daniel Fucking Quillen, Fields Medalist, Cole Prize Winner, architect of higher K-theory, conqueror of the Serre conjecture, and one of the intellectual giants of the 20th century!”
Arguably none of that has any place in a short note about a man gone briefly missing, so my gripe is not with the Gainesville Sun. My gripe is with the Universe. If I were running the Universe, there’d be some level of accomplishment that confers immunity from death, deterioration and obscurity. I’m not sure exactly where I’d set that bar, but I’m sure Dan Quillen would have cleared it.
Today is the birthday of the magnificent Emmy Noether, known as the “mother of modern algebra”, and one of my mathematical heroes. She is one of the few mathematicians in history who fundamentally changed what mathematics is about.
It was Emmy (I use her first name in order to distinguish her from her mathematician father Max) who first fully recognized the power of abstraction, which became the driving force of 20th century mathematics. She demonstrated time and again that it can be easier to solve a general problem than a specific one, and therefore the best way to attack a specific problem is often to generalize. Do you want to prove a fact about polynomial functions? First notice that polynomial functions can be added together, and they can be multiplied, and they obey certain laws along the way (like associativity and commutativity). Now prove a theorem that applies to anything that can be added and multiplied subject to those laws. Do it right, and you’ll replace intricate calculations with simple logical deductions. What was hard becomes easy. You get your result for free, and a whole lot of other results as a bonus.
Or, if you that doesn’t quite work, figure out what additional properties you’re using about polynomials, beyond associativity and commutativity, and prove a theorem about everything that has those properties.
To get a sense of how revolutionary this was, consider the Hilbert Basis Theorem, one of the foundational results of modern algebra. Have a look at Hilbert’s original proof — though you might not want to work through every detail in the 62 pages of equations and formulas. By contrast, Noether’s proof of a more general, more powerful and more useful version occupies all of one paragraph on Wikipedia.
Continue reading ‘The Art of Abstraction’
Bertrand Russell, that most rational of men, was nonetheless plagued by intermittent depression and the occasional nightmare. Including this one, as reported by Russell’s confidante, the mathematician G.H. Hardy:
[Russell] was in the top floor of the University Library, about A.D. 2100. A library assistant was going round the shelves carrying an enormous bucket, taking down books, glancing at them, restoring them to the shelves or dumping them into the bucket. At last he came to three large volumes which Russell could recognize as the last surviving copy of Principia Mathematica. He took down one of the volumes, turned over a few pages, seemed puzzled for a moment by the curious symbolism, closed the volume, balanced it in his hand and hesitated….
Principia Mathematica, to which Russell had devoted ten years of his life, was his (and co-author Alfred North Whitehead‘s) audacious and ultimately futile attempt to reduce all of mathematics to pure logic. It is a failure that enabled some of the great successes of 20th century mathematics. And — the first volume having been published in December, 1910 — this is its 100th birthday.
Continue reading ‘Lord Russell’s Nightmare’
 |
 |
 |
 |
Congratulations to the 2010 Fields Medalists, announced yesterday in Hyderabad. Elon Lindenstrauss, Ngo Bau Chau, Stanislav Smirnov, and Cedric Villani have been awarded math’s highest honor. (Up to four medalists are chosen every four years.)
My sense going in was that Ngo was widely considered a shoo-in, for his proof of the Fundamental Lemma of Langlands Theory. Do you want to know what the Fundamental Lemma says? Here is an 18-page statement (not proof!) of the lemma. The others were all strong favorites. Nevertheless:
Continue reading ‘Wikipedia Fail’
Today is the 209th birthday of Frederic Bastiat, the patron saint of economic communicators.
Of all the essays ever written, the one I most wish every voter could read and understand is Bastiat’s That Which is Seen and That Which is Not Seen. A boy breaks a window. Someone in the crowd observes that it’s all for the best—if windows weren’t occasionally broken, then glaziers would starve. This can’t be right, says Bastiat. If it were, we’d have no reason to diapprove of a glazier who pays boys to break windows. But why is it wrong? It’s wrong because it focuses on what is seen—six francs in the glazier’s pocket—and ignores what is unseen, namely the shoemaker who is deprived of a sale because those six francs come from what would have been the homeowner’s shoe budget.
Bastiat’s great insight in this essay is that exactly the same fallacy, in only slightly subtler form, underlies many of the public policy positions that were taken seriously in the 19th century—and, we might add, in the 21st.
Continue reading ‘Frederic Bastiat’
A month ago, I posted a portrait gallery of my personal heroes and invited readers to identify the faces; a few days later I posted the answer key.
To my mild surprise, the face that generated the most controvery—in both comments and email—was that of Abraham Lincoln, who was born 201 years ago on this day. Readers pulled no punches. ScottN wrote: “Lincoln is on a different list I have: People Who Caused the Most Unnecessary Deaths.” Peter wrote: “[Lincoln] was a tyrant and a racist to boot.” And the consistently provocative and thoughtful Bob Murphy wrote:
I would love to hear your reasons for including Lincoln. I have the same misgivings as the other commenter above, though I was going to introduce them with levity. (E.g. “I know you like math, Steve, so is that why you included the guy who maximized the wartime deaths of Americans?”)
I replied to Bob (and others) by email, with some sketchy thoughts and a promise to blog about Lincoln sometime on or before his birthday. With the deadline looming, I realize that I have little to add to those sketchy thoughts. So here, with only some minor editing, is the email I sent to Bob Murphy:
Continue reading ‘Ten Score and One Year Ago’
In a triumph of collective action, commenters have now managed to identify all of the personal heroes in my portrait gallery, either in comments to the original post or to the followup. For those who would like to check their answers, here is the gallery again, with full captions. After all the pictures, I’ve attached some brief commentary explaining who’s who and why some of these people are here. I’ll write in more detail about some of them over the coming weeks.
Yesterday I posted a portrait gallery honoring 60 of my personal heroes; readers were quick to identify 47, with remarkably few mistakes, all of which were quickly corrected. As of this writing, thirteen remain. Among these thirteen are the greatest mathematician of the 17th century (assuming we classify Newton as a physicist) and the three greatest mathematicians of the 20th; one of these is quite probably the greatest mathematician of all time. (All in my educated-but-not-fully-educated opinion, of course.) Musical, literary and cinematic greatness are also well represented here.
Over the next couple of weeks, I will try to tell you a little bit more about some of these 60 people. Meanwhile, here are the thirteen mystery men/women. I’ve retained the numbering from yesterday’s post. Who can you identify?
Continue reading ‘Unidentified Persons’
Since childhood, I have dreamed of someday having a house with a portrait gallery, where I would hang portraits of people I greatly admire. Every time I’ve either moved or redecorated, I’ve thought about dedicating a wall to this, but I never really had that much wallspace to spare.
A short time ago, it dawned on me that I actually have an infinite amount of wall space! My wall space is called the World Wide Web. And the World Wide Web is better than a physical wall, because the images are readily available (as opposed to hiding away in antique shops), and it’s easy to put things up and take things down, and you can share it with people you might not want to invite to your house.
So now I am prepared to unveil my World Wide Wall, or at least a first draft. I am well aware that many of these heroes are deeply flawed. I did not disqualify anyone for slaveholding, Louisiana purchases, Nazi sympathies or the imposition of protective tariffs. Not all of them are at the very top of their professions. The only criterion for inclusion was to make my heart go pit-a-pat.
My wall. Let me show you it. How many of these do you recognize? (No fair answering if you’re a personal friend who’s already seen an early draft of this.) And who would be on your wall?
Continue reading ‘The World Wide Wall’
In the theory of externalities—that is, costs imposed involuntarily on others—there have been exactly two great ideas. The first, forever associated with the name of Arthur Cecil Pigou (writing about 1920) is that things tend to go badly when people can escape the costs of their own behavior. Factories pollute too much because someone other than the factory owner has to breathe the polluted air. Nineteenth century trains threw off sparks that tended to ignite the crops on neighboring farms, and the railroads ran too many of those trains because the crops belonged to someone else. Farmers keep too many unfenced rabbits when they don’t care about the lettuce farmer next door.
Pigou’s solution—and it’s often a good one—is to make sure that people do feel the costs of their actions, via taxes, fines, or liability rules that allow the victims to sue for damages. Do a dollar’s worth of damage, and you’re charged a dollar.
Pigou endorsed this policy not because it seems fair, though it does seem fair to many, but because it yields, under what he believed to be very general conditions, the optimal amounts of damage. We don’t want too much pollution, but we don’t want too little, either, given that pollution is a necessary by-product of a lot of stuff we enjoy. Pigou offered a proof—now standard fare in all the textbooks—that his policies lead to the perfect compromises, in a sense that can be made precise.
The second great idea about externalities sprang full-blown from the mind of a law professor and subsequent Nobel prize winner named Ronald Coase, who stunned the profession in 1960 by pointing out that Pigou’s argument runs both ways. If you breathe the pollution from my factory, I’m imposing a cost on you—but at the same time, you’re imposing a cost on me. After all, if you lived somewhere else, you wouldn’t be complaining about the smoke and I wouldn’t be getting punished for it.
Continue reading ‘Happy 99th Birthday, Ronald Coase’
One hundred years ago today, Red Cloud, the last of the great Sioux warrior chiefs, died in peace on the Pine Ridge reservation at the age of 89. He was preceded in death by the way of life he fought so valiantly to preserve.
If there is such a thing as a just war, Red Cloud’s War of 1866 was more just than most. Black Kettle‘s village of peaceful Cheyenne had been recently and wantonly slaughtered by the Colorado militia under Colonel John Chivington at Sand Creek. (The survivors of this unhappy band would meet their deaths a few years later at Washita Creek, at the equally murderous hands of General George Armstrong Custer.) Against this background, the chiefs had been betrayed at Fort Laramie, where the government had summoned them to negotiate for the right to build roads through Indian territory. With the conference still in session and no agreement in sight, Colonel Henry Carrington and a force of 700 men arrived to build the Bozeman Trail.
