Can humans learn to see in more than three dimensions?
What follows is highly speculative (and therefore possibly nonsense), but bear with me. (Or, if you prefer, don’t.)
First, let’s think about how humans learn to see in more than two dimensions. Your visual cortex (at least as I understand it) is pretty much two-dimensional, but apparently your brain is pretty adept at converting two dimensions worth of information into a three-dimensional picture of the world around you.
To accomplish that feat, your brain employs (at least) two tricks. First, it can infer an object’s depth (by which I mean its distance in front of you) from the angle between it and your two pupils:
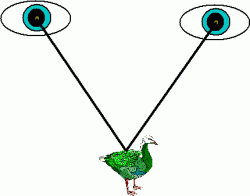
Second, your brain can infer an object’s depth from the size of the accommodation reflex (change in lens shape, pupillary contraction, etc) needed to focus on it.
Ordinarily, these two methods pretty much agree, and your brain uses that answer to construct its map of the world.
But suppose I could surgically adjust your eyes in a way that breaks that agreement. For example, the angle-method might continue to work just as it does now, but I’d disrupt the accommodation reflex so that your pupils now contract by an amount that depends not on the distance to an object but on, say, its redness, or its squareness, or even just varies randomly. Better yet, suppose I could do this at a very early age, when your brain is still learning how to process visual signals.