It’s often claimed (at least by politicians, journalists and their ilk) that affirmative action tends to “stigmatize” succcessful members of the favored group, in the sense that a Harvard professorship is less prestigious when it’s held by someone who might not have made it to Harvard without an affirmative action boost.

It’s approximately equally often claimed that this is effect is too small to worry about.

I’m not aware of anyone on either side of this argument having attempted to settle the question with arithmetic.

In their defense, the question can’t be settled by arithmetic, because it’s pretty hard to quantify the difference in “prestige” between a professorship that reveals you’re likely to be in the top one-one-hundredth of one percent of the population and a professorship that only reveals you’re likely to be in the top two-one-hundredths of one percent of the population. But we can at least give some answers contingent on different assumptions about this issue. (And contingent also, of course, on various modeling assumptions.)

To that end, here is a primitive first-pass model:

1. There is a prestige-conferring quality called “talent”.
2. All of the most talented people are funneled into one occupation, say “professor”. This means, in particular, that if you and I are identical except for the fact that you’re better at basketball, then I am (by definition) more talented than you, since you are more likely to become a basketball star and hence less likely to become a professor. Nevertheless, talent confers prestige.
3. Talent is distributed normally (or lognormally; it doesn’t matter because we’re going to fix the number of professorships, so only relative rankings matter).
4. The population divides into two groups. Let’s call them the Eloi and the Morlocks. Each has its own separate normal distribution of talent.
5. Although the Eloi constitute only half the population, they hold more than half the professorships. This is because there are more Eloi in the upper tail of the talent distribution than there are Morlocks.
6. A person’s prestige depends on that person’s expected percentile talent rank among the entire population, conditional on two observed characteristics: Is this person an Eloi? and Is this person a professor? We’ll call this statistic the person’s expected percentile for short.

Now we have a modeling decision to make: Why are there more Eloi at the top of the population-wide distribution than there are Morlocks? The two choices are:

The Sigma Model: The Eloi and the Morlocks are equally talented on average, but the Eloi have a higher variance.

The Mu Model: The Eloi and the Morlocks have the same variance in talent, but the Eloi have a higher mean.

It’s going to turn out (at least mildly surprisingly, I think) that the choice between these two models makes almost no difference.

Now we introduce an affirmative action program, requiring half of all professors to be Morlocks. This lowers the talent threshhold for a Morlock to become a professor (and raises the talent threshhold for an Eloi). Therefore the expected percentile of a Morlock professor falls, and so does the prestige of being a Morlock professor.

Question 1: By how much does affirmative action lower the expected percentile of a Morlock professor?

Question 2: By how much does affirmative action lower the prestige of a Morlock professor?

Question 1 is amenable to calculation. In fact, it’s a straightforward exercise (assignable to strong undergraduates!) to compute the answer to Question 1 in terms of three parameters:

• The fraction of Eloi (or Morlocks) in the population. Call this p. We fix the value of p (for now) at 50%.
• The fraction of the population who are professors. Call this variable t.
• The fraction of professors who are Morlocks. Call this variable r. We have assumed (see 5) above) that r < p.

(See here for some hints toward completing these calculations.)

Question 2, however, can’t be answered until we supplement our model with some assumption about exactly how prestige depends on expected percentile.

I find it easier to think about this question in terms of a variable I’ll call A, which is one minus the expected percentile. That is, if A equals, say, .01, then the average Morlock professor is in the top 1% of the population. If A equals .0001, then the average Morlock professor is in the top 1/100 of 1% of the population.

How does prestige depend on A? Here are two simple models:

Prestige Model 1: Prestige is measured by 1/A. For example, being in the top 1/100 of a percent of the population is 100 times more prestigious than being in the top 1 percent.

Prestige Model 2: Prestige is measured by 1-A. For example, being in the top 1/100 of one percent of the population is about 1% more prestigious than being in the top 1%.

Model 1 fits my intuition better than Model 2, but if your intuition begs to differ, I can’t prove you wrong.

It turns out (not surprisingly) that the choice of Prestige Model makes a huge difference for Question 2.

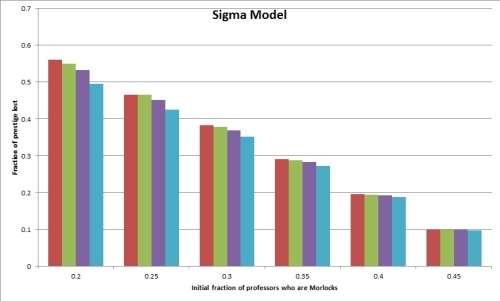
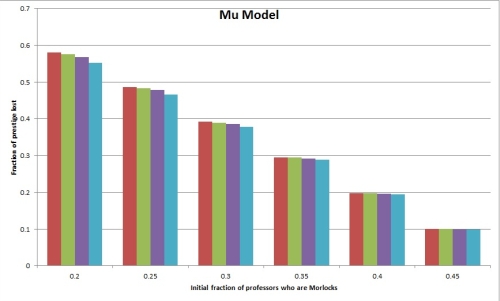
If we go with Prestige Model 1, here are some graphs that answer Question 2:

The labels on the horizontal axis correspond to various assumptions about the fraction of professors who are Morlocks in the pre-affirmative-action world. (We called this r.) The lower this number, the more dramatic will be the effects of affirmative action.

Each group of four bars represents the prestige loss to Morlock professors, on various assumptions (namely t=.00001, t=.0001, t=.001, t=.01) about the fraction of the population that are professors (and hence the amount of prestige that attaches to a professorship in the first place). The two graphs show results according to the Sigma Model and the Mu Model as described above; as you can see, the choice between these two models is pretty much inconsequential.

The main takeaway from these graphs is that for a Morlock professor, the prestige cost of affirmative action program is pretty enormous. When the Morlocks start out under-represented by half (so holding only 1/4 of the professorships instead of half), affirmative action cuts the prestige of a Morlock professor by nearly half. (Perhaps interestingly, this means that the total prestige of all Morlock professors stays about constant, since there are now twice as many of them.) Even if the Morlocks start out with 45% of the professorships (so that the affirmative action program is quite small), Morlock professors still lose about 10% of their prestige.

(This seemed surprising at first, but much less so in retrospect — if you’re roughly doubling the number of Morlock professors, you’re going to, on average, roughly double the value of A and hence roughly halve the prestige of being a Morlock professor. In the absence of some calculation, that’s not a complete argument, but it does indicate why the outcome makes sense.)

On the other hand, if we adopt Prestige Model 2 (where being in the top x% of the population gives you a prestige proportional to (100-x)), the prestige cost of affirmative action is near zero. For an illustrative example, take r=.25 and t=.001 (so that Morlocks hold 1/4 of the professorships initially, and you’ve got to be in the top 1/1000 of the population to be a professor). Then in the sigma model, the average Morlock professor is in the 99.9452 percentile before affirmative action and in the 99.8829 percentile afterward. On Prestige Model 1, that’s a prestige loss of about 53%. On Prestige Model 2, it’s a loss of about .06%. (The mu model gives very similar numbers.) So really, everything depends on how you measure prestige.

In an earlier thread, Jonathan Kariv observed that we might be able to hone in empirically on a prestige model by investigating the distribution of, say, Instagram hits among top celebrities. This seems to me like a good idea.

We’ve assumed that the Eloi and the Morlocks are equinumerous. What if we assume instead that the Morlocks are a minority, composing, say, 20% of the population? Here are some results for the Mu Model:

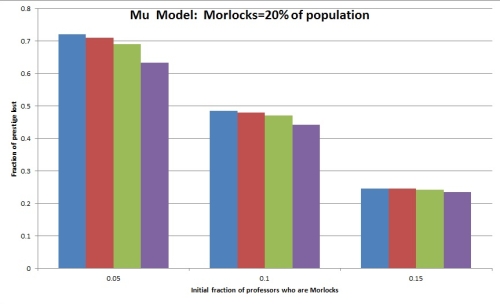
Here the horizontal labels correspond to the fraction of professors who are Morlocks (always under 20%) and we contemplate an affirmative action program that requires 20% of professors to be Morlocks. As before, the four bars in each grouping correspond to fractions of professors in the population of .00001, .0001, .001 and .01. And we get hits to prestige (measured by Prestige Model 1) extremely similar to what we get in the earlier case, where Morlocks are half the population. Conclusion: On this model, the “prestige cost” of affirmative action depends almost not at all on either the fraction of professors in the population (at least as long as it’s under about .01) and almost not at all on the fraction of Morlocks in the population.

I’ve computed Prestige(Expected Percentile). It might have been better to choose a prestige model and then compute Expected Prestige(Percentile), which is not the same thing. I think the current choice is defensible, and I prefer it at the moment partly (but not exclusively) because it defers the choice of a prestige model to the last possible moment.

I started this exercise with an essentially flat prior over what might turn up. (Translation: I had no clue what to expect.) I got a lot of surprises.

Surprise #1.It makes essentially no difference whether the under-represented Morlocks are 50% of the population or 20% of the population.

Surprise #2.It makes essentially no difference whether the under-representation is caused by cross-group differences in average talent or in variance of talent (i.e. the Sigma Model and the Mu Model give essentially the same results).

Surprise #3.At least above a certain threshhold, it makes essentially no difference how prestigious professorships are to begin with; varying t (the fraction of the population qualified to serve as professors) between .01 and .00001 has almost no effect on the (percentage) prestige losses.

Surprise #4.At least on Prestige Model 1, which I tend to think is reasonable (but could be talked out of), the prestige cost of affirmative action is much larger than I’d have guessed.

Non-Surprise #5.On Prestige Model 2, there is almost no prestige cost to affirmative action. (This, I think, should have been obvious even before calculating anything.)

What have I left out?

(Please note: There are dozens of arguments one could make for affirmative action, pro and con. This post is relevant to exactly one of those arguments. Please stay on topic.)