In 1706, the British astronomer John Machin calculated π to 100 digits (by hand of course). His trick was to notice that π = 16A – 4B where A and B are given by
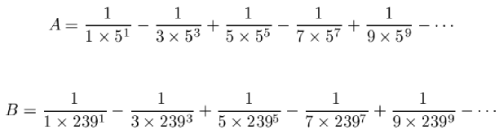
If you’re computing by hand, this is an excellent discovery, because the series for A involves a lot of divisions by 5, which are a lot easier to calculate than, say, divisions by 7, and the series for B converges very fast, so just a few terms buys you a whole lot of accuracy. (Try using, say, just the first four terms of A and just the first term of B to see what I mean.)
Machin’s 100 digits were a substantial improvement over the 72 digits obtained just a little earlier by Abraham Sharp, using the far less efficient series
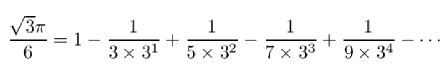
In 1729, a Frenchman named de Lagny got all the way to 127 digits, but, in the words of the scientist/engineer/philosopher/historian Petr Beckmann (of whom more later), de Lagny “sweated these digits out by Sharp’s series, and so exhibited more computational stamina than mathematical wits.”
Machin’s methods were ingenious, but no more ingenious — and certainly no more striking — than John Wallis’s 1655 discovery that
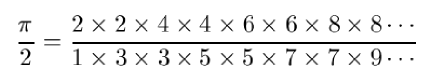
which still looks awesome to me after decades of familiarity.

