With a hat tip to Kenneth Anderson at the Volokh Conspiracy:
Golden Balls is a British game show where players decide, in secret, whether to adopt a strategy of “Split” or “Steal”. In this episode, they face the following payoffs (in British pounds):
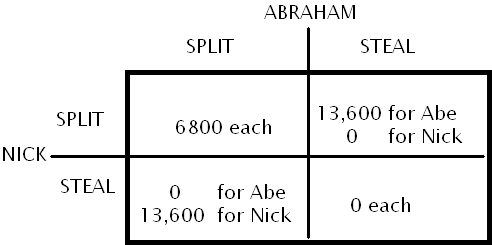
This is almost, but not quite a classic Prisoner’s Dilemma situation. (To make it a true Prisoner’s Dilemma, where stealing always beats splitting, you could change the lower-right hand box to “1 each” instead of “0 each”.) As in the Prisoner’s Dilemma, you can never go wrong by stealing — though you can go horribly wrong when the other guy steals, so it makes sense to reach a no-stealing agreement — and then to violate it.
In other words you’d pretty much expect homo economicus to steal every time. But this game is far more interesting than the usual textbook version of the Prisoner’s Dilemma, because it’s played by real people for real money and they negotiate in public for half a minute before they choose their strategies. In principle, the negotiation shouldn’t change anything (unless the players come to care about each other, or about the way they’re perceived by the audience). But in this episode, the negotiation took an unexpected turn.
What would you have done?



The lower left corner should read “13600 for Nick, 0 for Abe”.
The way the diagram is currently drawn, Abraham should always want to do the opposite of Nick
Are you sure you’ve got the payoff matrix right? The way you’ve written it, the top-right and bottom-left quadrants are equivalent.
Keith and Nitin: Thanks for catching this. I’ve fixed it.
Hey Steve, Paul Krugman is doing an AMA (ask me anything) on http://www.reddit.com/r/iama which is a forum where reddit users ask people from all different backgrounds questions. I would encourage you to consider doing one yourself. It may be a good outlet to promote the second edition of your book and generate some good discussion! If you are willing, head on over and private message one of the moderators. I love your blog by the way, took your intro class (favorite class I took in college – wish I had discovered econ before senior year), and am preordering the 2nd edition.
At one point, the host interrupts, “There is no legal requirement for him to split the money with you.”
That’s what I wondered about. Could they have both taken out a sheet of paper and written, “The undersigned both agree that they will pick ‘Split’, and if they violate this agreement, then they have to pay the other party any prize that they win”? I wonder if they have to sign something before the show saying that they *won’t* engage in legally binding contracts during the in-game negotiations.
I always wondered that about shows like “Survivor” as well. If I’d been on the island, I would have gathered everyone for a meeting and said, “Look, let’s just all sign a binding contract right here saying that no matter who wins, we all have to split the prize money equally. Then we can spend the absolute minimum effort doing things like eating rats and running through swamps and whatever other degrading things the producers come up with, and we can vote each other off more or less at random, and in the end someone has to win anyway.”
I suppose that would have only worked for one season, and thereafter the producers would have prohibited that kind of “anti-competitive” behavior in the waivers contestants have to sign. But I wonder if they thought of it from the very beginning.
Bennett, given that the show is not live, I don’t think tricking the producers is going to work. And most “reality” shows, particularly ones like Survivor, are staged to varying degrees. Otherwise they’d be a lot more boring.
Correction: I should say, the show is not aired live.
Seems like an obvious tactic in that situation, at least now that everyone’s seen it. If Abe had thought it through & been prepared for the likelihood, he could respond by stealing. (Then split the money informally?) Or, both could try to convince each other they’re going to steal.
This is absolutely brilliant. It will be shown in class.
Wonderful. But I think it’s Ibrahim not Abraham.
I was waiting for Ibrahim to say. “How about I steal and you split and I split the money with you”.
We find out that Nick is trying to prevent the steal-steal case and does essentially by breaking the symmetry of the game. No reason Ibrahim can’t do the same. Of course this forces this into a game of chicken with both parties somewhat annoyed at each other come “splitting time”.
Is there a rule against trading balls? Wouldn’t that guarantee a split payoff?
@Alex S:
You mean we pick, then swap? Won’t work. I pick STEAL and pass it to you.
You mean we swap first, then pick? Either one of us has to pick STEAL or the situation is unchanged. That won’t work either.
Brilliantly executed on both parties…by both players! That was fun to watch! Kudos to Nick (the black guy) for playing rationally given the revealed strategy of Abraham (the seemingly crazy, yet brilliant, white guy).
This was a truly amazing strategy: it pretty starkly reveals that human interests are not purely for simple monetary gain, but also incorporate elements of people’s interests in perceived self-worth and public identity, which are often at least as important to many people as the potential winnings on the table. Players can manipulate and appeal to those aspects as well (as well as lying about them! One can portray themselves as valuing honesty and integrity more than the money, and yet be lying about that… and yet in the end STILL be lying about that in order to gain the mutual benefit: so incredibly complex!). Economics and game theory have as much to say about how those elements factor into strategies as they do about pure rational self-interest. It’s a far more complicated game when those aspects are taken into account, but it’s still a game worth modeling for insight.
Also, +1 for Prof. Landsburg doing one or many AMAs. Reddit has some pretty well-known political biases, but it also has a lot of very bright and libertarian-leaning folks.
Drew – do you have a link to that reddit AMA?
@Ken B
I meant we agree beforehand to pick then swap. Knowing that whatever I pick will end up with you, why wouldn’t I automatically pick split? And same with you.
One does not simply promote their second book in an AMA.
I’m a little confused – the first thing that both participants do is look at BOTH balls. If there are two balls and you look at one that happens to say Split, aren’t you certain the other one says steal? Are they really skeptical enough to question that?
What does Ibrahim say at the very end?
I think I heard “With the money I won, I think I’ll respray my yacht”. Nick gives a very surprised look upon hearing it.
Crud, this is exactly the strategy I’d decided I would use if I were ever on one of these shows (except I hadn’t thought of the brilliant put ‘share’ down anyways; which might prevent me from having to report more earnings on taxes than I actually ended up with) but now that it’s out I have a higher chance of playing against someone with the same strategy — which would be really entertaining to watch but would probably end up disastrous for me!
@Alex S: Oh, now I see what you mean. Sorry, slow of me. You mean basically I make your choice and you make mine, by agreement, through the mechanism of ball-swapping. Of course, then I ‘know’ you will pick swap so I pick steal but then refuse to trade balls, just like Nick could refuse to share.
Nick’s clever point was, he refused to trust Abraham (he said) so forced Abraham to trust him. Of course he then trusted his manipulation of Abraham!
@ Ken B
Yes you’re right. There’s still an enforcement problem, but if you can use the host as an escrow agent, you can address it ex ante.
In a game of chicken, one strategy is to conspicuously throw your steering wheel out of the window. In this manner, your opponent learns that that you’re not going to swerve, and therefore the opponent is confronted with the choice of swerve or crash. The white guy engaged in precisely this behavior.
Wikipedia notes this strategy in discussing “Chicken (the game).”
While I generally favor maximizing choices, I acknowledge that people can benefit from having their choices limited. The Hatch Act constrains a federal employee from engaging in campaigning – on the theory that this is the best way to keep these employees from being coerced into campaigning. We adopt similar policies regarding prostitution, statutory rape, child labor, etc.
Now consider the intersection of two hot-button issues: health insurance and same-sex marriage.
Insurers want to avoid adverse selection – ending up with a pool of insured customers that have disproportionately expensive medical needs. One way to avoid this problem is to test all applicants – but that’s expensive. Another way is to insure large pools of people who were picked on some basis that is uncorrelated with – or is negatively correlated with – bad health. Employed people fit the bill; insurers know that employed people tend to be at least as healthy as the population at large. And even if an employer wanted to extend health insurance to a friend, insurers know that employment relationships tend to be sufficiently complicated to unwind that few employers will create such relationships purely for philanthropic reasons; “barriers to exit” are too high.
In addition, insurers are willing to extend health insurance to the spouses of employees. Insurers know that employed people don’t generally pick unhealthy people as spouses. And even if an employee wanted to extend health insurance to a friend, marriage is a sufficiently burdensome activity to unwind that few people engage in it for purely philanthropic reasons; “barriers to exit” are too high.
Assuming homosexual people are also prone to marry healthy people, would insurers treat same-sex couples in the same manner as male/female couples? The answer may depend upon whether the couple has gotten married in a state that recognizes same-sex marriage. The act of acquiring state recognition helps create those barriers to exist that reassure the insurance company that this relationship is probably not created simply for the purpose of securing health insurance. But in the absence of state recognition of the relationship, the barriers to exit are lower – and the insurance company may be less willing to extend health insurance to the spouse. In other words, where members of a same-sex couple have MORE options to leave the marriage, they are made WORSE off – at least when seeking health insurance from a spouse’s employer.
(Or so I was told. Now that we have varying state laws on the subject, I wonder if we’ll see disparities in the behavior of insurance companies.)
The “Steal, and split after the show” strategy has a potential tax disadvantage if Abe is taxed on the full amount, and a gift to Nick is taxed as well (assuming the rules of the game rule out the ability to contract at law, i.e., say that no prize will be awarded unless the participants agree that they have no enforceable contract etc.)
In that light, Abe’s strategy is even more impressive. He minimizes the joint tax burden to boot.
My approach would have been similar to AlexS’s. I would get up and rotate the golden ball tray 180 degrees. So in effect A chooses for N and N chooses for A. If you are picking for your opponent, your only incentive here is to pick Split.
I’m assuming, of course, that the show’s rules allow for this.
Nate C,
I’m a little confused – the first thing that both participants do is look at BOTH balls. If there are two balls
There are four balls all together, two for each contestant. In this case Abe doesn’t know which of Ibrahim’s balls says “SPLIT” or “STEAL” and vice versa for Ibrahim. The contestants were asked to check their own balls to make sure that one says “SPLIT” and the other says “STEAL”.
@Economiser: Your scheme does not work, as you can only tell what is in the ball by opening it.
Note that Nick’s little bit of manipulation works within the rules as stated and does not require anyone trust Jasper Carrot.
@ Nobody.Really
Lmao. You’re the reason I read this blog (the Armchair Economist aside).
Refreshingly random.
Nate C: I chuckled when they did that. Better safe than sorry I guess.
Very nice.
One argument Nick could have used (and I was a little surprised he didn’t) was that he would surely be reviled and chastised — possibly much worse — if he didn’t honor the side deal. There is a natural assumption that the “negotiating” done “in the show” is separate from external agreements. Nick is essentially making a deal outside the bounds of the show (clearly, because there are no elements of the show binding him to this agreement), and as such his real world reputation is at stake — not his game show reputation.
There are many people who see these as different things, and perhaps rightly so. The audience would see it as clever if one of the guys argued to get the other to do split and then stole without making any such outside agreement. They wouldn’t see it as a betrayal or breaking of any contract that the wronged party had any right to assume. But, by stepping out of the realm of the game, Nick really is putting his real world reputation on the line, and given the highly public nature it is more reasonable to assume that he would honor this agreement than any simple statement about how he would choose “split”.
I would like to think I would have had the idea to do what Nick did. And, were I in Abraham’s shoes, certainly would have chosen Split.
THIS is why people want politicians that lie to them. The repeated game result of this is people will vote for for politicians that are both liars and say things we do not agree with.
If you’re suggesting that voters care more about good outcomes than about good conduct, I suspect you’re right. Consider two quotes:
Moreover, there are systemic reasons to suspect that lots of people who rise in hierarchies do so while lying. Politics provides a well-studied example.
First, there’s the well-known “Etch a Sketch” phenomenon of politicians engaging in one type of campaign to secure their party’s nomination, then engaging in a distinct campaign to win office.
Second, think of political races as auctions: Politicians are bidding for your vote, offering increasingly enticing promises. What would a politician bid? Even the sincerest politician may be mistaken about what he can accomplish while in office. So a bid might equal [amount politician believes he can deliver] + [error term].
If we imagine a field of politicians who are equally able to deliver, the one who would win the auction would be the one who has the biggest (positive) error term. The more politicians vying for a seat, the greater this likelihood becomes. If you imagine a field of politicians with unequal ability to deliver, the two qualities that would help the politician win would be 1) the politician’s ability to deliver and 2) the politician’s lack of awareness about his inability to deliver. Thus, merit matters, but so does a bold ignorance.
Over time, voters would experience a stream of politicians that promise more than they could deliver, even assuming the politicians were earnest. And thus, the public would come to expect falsehoods from politicians (just as experienced bidders at auctions may come to discount their estimate of the value of an auctioned item, recognizing that auctions are designed to produce “buyers remorse”).
This dynamic assures that virtually every successful politician, no matter how earnest, will have promised more than he could deliver – and yet was rewarded. (To be sure, plenty of unsuccessful politicians also promised more than they could have delivered, too.) Thus, successful politicians receive powerful reinforcements for dissembling. And as politicians rise in the hierarchy, this reinforcement compounds. Combine this dynamic with the idea that the public come to expect dissembling from politicians, and the incentive structure becomes pretty powerful.
“THIS is why people want politicians that lie to them.”
Another sad confusion about Bayes’s theorem. When 99.9999% of the sample lies just as a matter of course ….
@Ken B: That doesn’t invalidate my scheme. I expect the competitors to look at each ball. What I’m saying is: you choose for me, and I choose for you. In that case the payoff matrix is flipped on its head and each contestant has no incentive to select “steal.”
Nick’s manipulation worked because he made what Ibrahim viewed as a sincere threat at that time. Now that Nick played the strategy in public, and was revealed to have lied, any future player trying the same strategy will have a harder time convincing his opponent that he is sincere. If I were Nick 2.0 attempting the same strategy, I might consider opening up the “steal” ball and showing it to my opponent so he knows I am not lying. That’s the equivalent of actually ripping out the steering wheel in a game of chicken, as opposed to merely saying that you will.
@Economiser:
Your scheme was ” I would get up and rotate the golden ball tray 180 degrees. So in effect A chooses for N and N chooses for A. ”
So still no-one sees all 4 balls.
What can this plan entail? Either the rotation occurs before the peeking, in which case it makes no difference, or afterwards but before the choosing, when the ball chooser is then ignorant of the balls in front of him. Or after the choosing, and that is your private ‘trust me’ deal.
Are you saying, Abraham trust me, I’ll rotate after we choose? Then you could still pick steal and rotate that.
To evade that you need a mechanism and your proposal doesn’t do it.
There are lots of ways to deal with games that are not this game.
@KenB:
I think we are talking past each other. My proposal is: I am giving you the ability to select my strategy, and in return you are giving me the ability to select your strategy. Rotating the ball tray is a physical manifestation of the proposal but is not necessary.
For example, if you and I were playing the game, I would get to decide if you, KenB, steal or split. In turn, you, KenB, would get to decide if I, Economiser, steal or split. I’m giving you my choice in exchange for you giving me your choice.
Given the amount of time it has taken to explain this, perhaps it wouldn’t work under the TV show’s time constraints.
While he was able to pull it off impressively, I don’t think his strategy was incredible. I saw it more as a read on another person. If you’re Nick you have to be 100% certain the other player will not come over the top and say, no, you listen to me Nick.
If Nick were playing himself is the strategy all of the sudden great. It’s only good because he could key in on the fact that he could bully Abe.
If Abe had “played” dumb and acted just as he did but played STEAL, we would be calling him the brilliant one. Nick did not reinvent the wheel here. This situation speaks more to the beauty of the prisoner’s dilemma than it does of any prisoner.
While its obvious that in a GTO sense, always choosing steal is of course correct, and this is a trivial problem. But you are dealing with human beings, and all the value in the scenario lies in your ability to convince him to bet split.
The guy in the video ALMOST has the perfect strategy right, imo. I think, as long as its allowed, the true perfect strategy is to instantly say, once negotiations are open:
“I am 100% going to pick steal. I will give you 1,000 pounds after the show if you pick split, obviously we get nothing if you pick steal. This is not a negotiation.”
And then you INSTANTLY stick your fingers in your ears, close your eyes and hum as loudly as you can.
You give the other guy 30 seconds to figure out that he is now choosing between CERTAIN nothing, or a POSSIBILITY of 1,000 pounds. He has to decide whether the satisfaction he gets from punishing you is worth 1,000 pounds. Pick the number (1,000) accordingly based on your best guess of his spite equity.
Obviously the decision to then split after his ultimatum is insanity.
@Economiser:
FWIW, I got your proposal immediately and thought it was a good one, or at least interesting. The incentive to pick steal seems like it must go down. Then again, people find creative ways to maximize their takings.
“I wonder if they thought of it from the very beginning”
About survivor-type shows, I think the whole setup prevents collaboration. Less through rules and incentives and more through selection. They are going to pick participants that are ambitious, competitive and aggressive. The successful game-show must create tense dynamics, and people naturally prone to collaborate would not give them that.
@Chad:
The problem with your strategy is: what happens if both pursue it? The optimal strategy, if one exists, must take into account different responses from the opponent.
Here’s an interesting phenomenon :
Tell an intelligent person “Here’s a great video, showing an amazing strategy in a prisoner’s dilemma problem!!” and 100% of the time, they quickly figure out that the strategy is to convince the other player they’re going to ‘steal’, and to make it worth their while to choose ‘split’, eg, by offering to share some of the cash.
Admittedly, when I say 100%, my sample size is only two. Can anyone add some samples? Do intelligent people, being told there’s an amazing strategy, guess it (except for the twist) before watching the video?
@Mike H:
No. Because it is, in fact, not a brilliant strategy at all. It’s one of many strategies that could be employed correctly and seem brilliant ex post.
What am I missing? Once Nick convinced Ibrahim to Split, why didn’t Nick just steal and keep the money? If I were Ibrahim, I would never have agreed to split. I would’ve told Nick to let me be the one to pick steal and he could pick split.
@Phil, I respectfully disagree. The brilliance of Nick’s strategy is that it takes a prisoner’s dilemma and changes it into an altogether different game. For Ib, the payout matrix became :
Nick Splits : 6800, 13600
Nick Steals : X, 0
where X is less than 6800, but more than 0.
Before, if Ib is thinking of splitting, he can only improve things if he chooses to steal. He can’t make things worse.
After Nick’s statements, if Ib is thinking of splitting, he might in fact make things worse if he changes his mind. It depends on his estimate of the likelihood of Nick stealing. Nick was quite convincingly able to persuade Ib that this probability was close to 100%.
The logical thing to do is then for Ib to ‘split’. He doesn’t have to fully trust Nick in anything for this to be the case – If he only half trusts Nick to share the prize, and thinks Nick will choose ‘steal’ with just 3:1 odds, it’s still best for him to ‘split’.
Changing a prisoner’s dilemma into something else is a brilliant strategy. If you don’t think so, please explain why action on climate change is so politically hard.
Adam: As said by others, Nick extended the game to emphasise his “real world” reputation. If he had chosen steal, he would have been £6800 richer, but his reputation for honesty would have suffered. He could have stolen and given Ibrahim the money afterwards, but the audience may not know he had done that. However, he chose to split, and demonstrate to everyone that: A) he is an honest man and also B) he is good at negotiating. If Ibrahim had chosen to steal, Nick would have looked a bit of a prawn. By choosing split, Nick demonstrated that he was both honest and confident that he had got Ibrahim to do what he wanted.
@ Henri: Thanks. I like Nick’s strategy better perhaps but I did not think of it before watching the video.
@Chad: I like your response. I would take it a step further and show my opponent the “steal” ball. That way he _knows_ I am stealing, instead of having to take my word for it (which is the Nick strategy).
Also I would probably do what Nick did and offer half the prize. Game theory in the real world is often about emotion, not logic. Even though a rational actor would choose GBP 1,000 over 0, many real people would feel cheated and would take 0 out of spite.
Economiser: “Game theory in the real world is often about emotion, not logic.”
Yup. Emotions which are about playing repeated games. As I have noted before, it is almost impossible to get people to play one-time games, for this reason. And in the lab it’s not clear they really are just playing the game one time (will people truat the experimenter 100%?), or are playing just that game. For instance, people are always aware they are being judged by the audience, or the experimenter, or their future selves.
I agree with AlexS:
The best strategy is to propose to the other player to pick strategies for each other. I pick a ball and hand it to you to be opened when the host gives the signal; you pick a ball and hand it to me to be opened when the host gives the signal. It should be clear even to people who haven’t studied game theory that each player’s self-interest dictates that he/she pick “Split”.
Would there be an enforcement problem (or would enforcement require the action of a third party)? No.
An enforcement problem would only arise if you could not trust your own eyes (that is, if there were a way to be deceived about whether the other player is opening the ball I handed him/her). When I give you my “Split” ball to open, I’ll only stick to our agreement to open the ball you gave me, if I’m 100% certain – that is, when I observe – that you are actually opening the ball I gave you. So I can make my cooperation conditional on observing your cooperation. If I think that somehow you managed to exchange the ball I gave you (a “Split” ball) against the one you kept (a “Steal” ball), I can just demand that we engage in another round of picking strategy for each other.
If the other player does not accept this proposed strategy I’d just play “Steal”.
I also agree that Nick’s strategy is quite ingenious. However, it does require that either a) Ibrahim trusts Nick to some degree or b) doesn’t consider the outcome “Nick steals, I split, and Nick doesn’t split the money” as the absolutely worst outcome. Regarding b), Ibrahim could reason: Yeah, I’d like to split with Nick, but I have no clue whether he’ll keep his promise to split the money with me after the show AND I would really hate to end up as the sucker!
In other words to play “Steal” you don’t have to be stupid or greedy. It’s enough to doubt sufficiently strongly that your opponent will play “Split” AND to desire not to be the sucker in the game.
Ergo: Nick played in a clever way but he could have lost if either a) Ibrahim had not trusted him to some extent or b) with Ibrahim not trusting Nick at all, Ibrahim had preferred not to be the sucker, i.e., prefering taking the risk that both lose over the risk that only he himself loses (= being the sucker in the game).
As far as I can see, the strategy proposed by AlexS doesn’t require any trust because whether a player sticks to the agreement or not is observable.
From the wikipedia entry for the show:
“Golden Balls has attracted attention from social scientists as a natural experiment on cooperation. A team of economists including Richard Thaler have analyzed the decisions of the final contestants and found, among others, the following …” (http://ssrn.com/abstract=1592456)
Clicking on this link should bring you to the paper mentioned in the comment just above this one (it’s the same as in this comment except for a bracket at the end):
http://ssrn.com/abstract=1592456
Mike H:
The strategy is not brilliant, not even clever, for the reason I outlined above.
He didn’t change the game at all. What’s to prevent Ib from saying, no, Nick, you listen to me. ” I AM GOING TO STEAL. YOU back down, you pick split, and guess what I might give you 1/8, because the expected value of Prize/8*I’m not screwing you is still better than 0.”
If I’m Ibrahim I say, hey Nick we can talk all day. But here’s my split ball, see, and I throw it across the room. There’s no reason Ibrahim cannot turn the table on Nick, and so Nick’s genius was his his read of Ibrahim, not his strategy.
Nick doesn’t better his chances. He still has to rely on Ibrahim to go along otherwise he could end up with 0.
@Phil “What’s to prevent Ib from saying…”
Given what Nick had already established halfway through the negotiations, that would have been irrational behaviour on Ib’s part.
@ Mike:
There are two ways I think you’re potentially misunderstanding.
1. If you think Nick did well aggressively putting Ib on the spot, then it’s not the strategy that is great. Strategies are understood out of context, not in the context that you have a bully and a duck.
2. It’s not irrational for Ib to try to turn the tables if it wasn’t irrational for Nick to do what he did in the first place. If Ib turned out to be a bigger bully and can say I heard what you said, I’m stealing it would make Nick’s choice to steal irrational. We don’t attribute Nick with irrationality and so you cant say Ib would be. There’s nothing special about being first to the poll unless Nick actually shows Ib that he has thrown away split, Ib can mirror the tactic
It still is clearly prisoners dilemma until Ib ultimately proves himself to be a duck who has been outplayed. But that is the context of this particular match, not anything to do with the general strategy employed. It’s a dilemma for a reason.
PB: thanks for the link to an interesting paper.
1) Despite the fairly obvious conclusion that stealing cannot make you leave the show with less that splitting would, splitting is quite common. In 31% both split, 44% one split and 25% both stole. People are either not able to work out that splitting cannot make you better off, or they are valuing something else quite highly. AS Ken B says, contestents are not playing a one-shot game. The clip shown above shows that Nick values “winning” the game above taking home more money. For him, winning meant a succesful cooperation. For others, winning might mean succesfully suckering the other one.
2) The “small peanuts” effect. When playing for “small” stakes of a few hundred dollars, people were much more likely to cooperate. This is interpreted that they would rather be seen as cooperating than win such a small sum. However, the sum would be considerd large in most contexts, and huge compared to sums used in university research. This “context” effect disppeared at £1500, above which cooperation rates were unrelated to prize money.
3) There was significant “reciprocal” tendency not to cooperate with those who had tried to get one voted off in earlier rounds.
4) There was no evidence of expectational conditional cooperation. Either people could not predict cooperation, or they had no reciprocal tendencies. Given the strong reciprocal tendency above, it seems that people could not predict who was going to cooperate. However, saying that you were going to split was the strongest predictor of whether you actually did – those who made an explicit promise to split were 33% more likely to do so. Since people could not predict who would split, it seems we are missing out on an obvious source of information – that people often do what they say.
Regarding the dispute between Mike H and Phil King: I’m siding with Phil.
One interpretation of Nick’s strategy is that he changed the game from a prisoners’ dilemma into a chicken game and then did the equivalent of throwing away the steering wheel by committing himself to the “Steal” strategy, leaving his opponent no option but to play “Split”.
This view is wrong because what matters to Ibrahim is that Nick cannot credibly commit himself to splitting the money after the show just by announcing his intention to do so. The game Nick and Ibrahim are playing cannot be turned into a chicken game in the way Nick proceeded because Nick had no way to force himself to split the money after the show.
How could Ibrahim know that Nick will really split the money with him? Nick’s strategy could simply be a clever but risky way of persuading Ibrahim to play “Split” so that he, Nick, can walk away with the whole jackpot himself.
Nick made an attempt to force Ibrahim to trust him. In response, as Phil argued, Ibrahim could have reasoned: I don’t like being forced into trusting Nick; I’m proposing that I’m playing “Steal”, and you Nick play “Split”, and I’ll split the money with you after the show. Remember that once you have persuaded your opponent to trust you, you face the temptation to double-cross him. That’s the devilish logic of the prisoners’ dilemma. One of the key definitional characteristics of this dilemma is that the players cannot make credible commitments – that is why allowing pre-play communication between the players does not change the logic of the prisoners’ dilemma. (In real life, the possibility of pre-play communication between the players does change the way people play the game, but the strategy/outcome matrix does not change. The players can still attempt to double-cross each other: Just go to youtube and watch a few clips from this show.)
After Nick has announced his ultimatum Ibrahim’s choices are as follows:
1. He can accept that Nick will play “Steal”, in which case Ibrahim’s chooses between:
– “Not being the sucker (only loser)” for sure, by playing “Steal” and,
– a lottery with 2 outcomes (given that Ibrahim cannot know whether Nick will keep his promise to split the money after the show): winning half the money or being the sucker/only loser, by playing “Split”
2. Ibrahim could also counter Nick’s ultimatum with the proposal that he, Ibrahim, will play “Steal” and Nick play “Split”, and he promises to split the money with Nick after the show … and then Nick and Ibrahim try to bully each other into playing “Split” while promising to split the money after the show (without being able to commit themselves to keep the promise).
So after Nick has announced his ultimatum, Ibrahim is in the SAME position as before. He can play either “Split” or “Steal”, and he can end up as the only winner, the sucker/only loser, with half the money, or with no money while Nick doesn’t win any money either. Ergo: Nick’s ultimatum changed nothing.
Nick played the game with ingenuity but his strategy did not change the type of game they were playing. It could have ended differently for him if he had played against another opponent.
Abe/Ib deserves some credit for trying to make it “OK if I’m gonna be the sucker, you’re not a MAN”
PB: I agree that Nick did not change the game. What he did was, however, clever. The paper shows that promising to split does not convince the other player that you will do so (even though it is often true). What Nick did was a more convincing promise that he would steal. Promising to steal turned out to be convincing, and the promise to pay after the game raised the “reputation” stakes. The fact that many people split shows that this reputation element is quite strong.
The point is that a promise to split is not convincing, but a promise to steal is. Interesting.