There are two kinds of people in this world: The first kind wonders why people stand still on escalators but not on stairs. The second kind wonders what’s wrong with the first kind. After all, if you stand still on the stairs you never get anywhere.
But people of the first kind are not usually dumb. I could give you a long list of top-rate economists and mathematicians who have been stumped by this puzzle. But I could also give you a long list of equally smart people who have been stumped by why anybody thinks it’s a puzzle in the first place. It’s come up again several times recently, because I included it in Can You Outsmart an Economist? and because I talked about it on my podcast with Bob Murphy, which generated a small flurry of email from listeners. So let me try once again to explain what’s going on here.
Let’s divide this into two parts: First, what’s the right way to think about this problem? Second, why is it a problem in the first place?
Assume that all escalators are 100 yards long, all staircases are 100 yards long, all escalators travel at 10 yards per minutes and all walking speeds are 10 yards per minute — so if you walk on an escalator, you progress at 20 yards per minute. (You can change these numbers to anything you like without affecting any of the logic to follow).
Every day, Alice takes the escalator and then the stairs, while Bob takes the stairs and then the escalator. They both always walk, so they each spend 5 minutes on the escalator and ten minutes on the stairs, arriving at their destinations in fifteen minutes.
Resting-Alice is exactly like Alice, except that she always spends her first minute on the escalator resting. Resting-Bob is exactly like Bob, except that he always spends his first minute on the stairs resting.
The question is: Is it better to emulate Resting-Alice than to emulate Resting-Bob, and if so why?
First, let’s compare the progress of Alice and Resting-Alice:
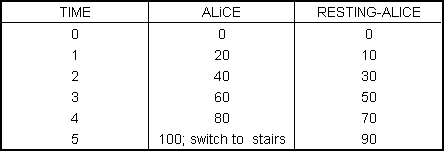
As you can see, Resting-Alice’s break leaves her 10 yards behind Alice, and long after the break is over, she’s still the same 10 yards behind.
Now let’s compare Bob with Resting-Bob:
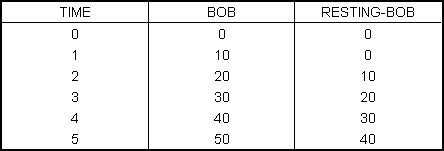
As with the Alice’s, Resting-Bob’s break leaves him 10 yards behind Bob, and long after the break is over, he’s still the same 10 yards behind.
It appears, then, that Resting-Bob and Resting-Alice have each paid the same 10-yard penalty for their sloth, and there’s no reason to consider either of them wiser than the other.
That is in fact the wrong conclusion. But to see why, it’s not enough to think about what happens 2, 3 or 4 seconds into the game. You have to look way ahead, to the time when people start switching from escalators to stairs and vice-versa. If you continue the charts forward, you’ll see that while Alice switches to the stairs at time 5, Resting-Alice switches to the stairs at time 5.5. That gives Resting-Alice an extra .5 seconds on the escalator, during which she can partially catch up to Alice, narrowing the gap from 10 yards to 5:
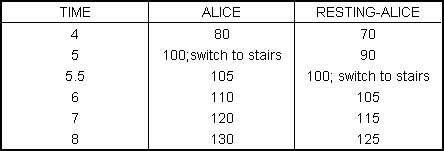
If you expand the Bob-chart forward, you’ll see that while Bob switches to the escalator at time 10, Resting-Bob doesn’t switch to the escalator till time 11, which gives Bob time to expand his lead from 10 yards to 20:
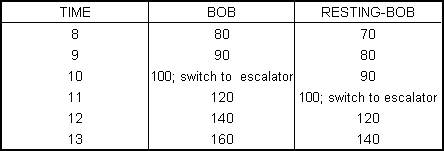
So if you’re going to be either Resting-Bob or Resting-Alice, it does make more sense to be Resting-Alice after all.
Now to the main question: Should this have been obvious all along?
Many people say yes, it was obvious all along. But in my experience, they often defend that position with rhetoric along the lines of “If you rest on the escalator, at least you’re making progress”.
People who say that are definitely wrong. Because the resolution of the problem has nothing to do with what happens while you’re resting; instead it has to do with what happens long afterward, when you switch from the stairs to the escalator or vice versa.
To see this most starkly, imagine that Alice and Resting-Alice get on an infinite escalator and stay on it forever. Alice starts walking from the get-go, while Resting-Alice stands for a minute before she starts walking. Bob and Resting-Bob do the same on an infinite staircase. Then Resting-Alice will be ten yards behind Alice forever, and Resting-Bob will be ten yards behind Bob forever. As long as the only relevant variable is the resting-time, and as long as you measure progress in yards, it is not true that Resting-Alice has made a wiser choice than Resting-Bob. So if your argument applies equally well on an infinite escalator as on a finite one, your argument is wrong. And if your argument is phrased in terms of things that happen during or immediately after the resting phase then your argument applies equally well on an infinite escalator, so your argument is wrong.
The key difference between Resting-Alice and Resting-Bob has nothing to do with what happens while they’re resting, and everything to do with the (much later) catch-up period when people are switching from the stairs tot he escalator or vice-versa. Any argument that ignores this is a bad argument, even if it reaches the right conclusion. And any instinct that says “This is too obvious to think about” based on an intuition about what happens during the rest period is a bad intuition. So anyone who says “When you rest on the escalator at least you’re moving” is making a bad argument that just happens, in this particular case, to yield the right conclusion. We don’t usually give credit to students who conclude that 64/16=4 by “canceling the sixes”.
Suppose Alice rests on the escalator while Bob rests at the bottom of the stairs, and that they both rest until the moment Alice gets off the escalator. Alice says: “Ha ha! I’m on the second floor and Bob’s still on the first. Obviously it’s better to rest on the escalator than on the stairs!”
But Alice is totally wrong to make this argument. All she’s shown is that it’s better to take the escalator than to take the stairs. That’s true, but nobody ever disputed it. And it’s equally true whether or not you’re resting, and has nothing to do with whether you rest.
After all, when Alice gets off the escalator, she is exactly as far behind all the other people who rode the escalator as Bob is behind all the other people who took the stairs. Her rest period and his rest period were in that sense equally costly.
Again, there are two components to this problem. First is the “local” component: How far do you fall behind when you rest? Answer: You lose 10 yards. That’s true for Resting-Bob, it’s true for Resting-Alice, and it leaves no reason to prefer one strategy to the other.
Second is the “non-local” component: What happens long after the resting period, when people make their switches from one mode of transport to the other? That’s where Resting-Alice gets more time on the escalator and catches up.
Now for many many optimization problems, the key is to focus in on the local effects. Ninety-nine percent of the time that strategy pays off. And if you’re in the business of thinking hard about optimization problems, you gain an instinct for focusing in on what’s local, and 99% of the time you get rewarded for that. Occasionally you get led astray.
For other equally smart people who don’t happen to spend their lives thinking about this kind of problem, the trap is never tempting, they never fall into it, and they can’t understand why anyone would fall for it in the first place. But that’s not because they have a better way of thinking; it’s because they trust their instincts, which just happen to lead to the right conclusion in this particular case, though, as far as I can see, for entirely wrong reasons.
I claim that the First Kind of Person typically thinks correctly about what happens during the rest period, forgets to think about what happens during the catch-up period, and therefore reaches the wrong conclusion, and then are often troubled because the conclusion seems wrong.
I claim that the Second Kind of Person typically thinks incorrectly about what happens during the rest period, forgets to think about what happens during the catch-up period, and therefore happens (by pure luck) to reach the right conclusion, and then are puzzled about how anybody could have gotten this wrong or believed it was hard.
Of course there is also the Third Kind of Person, who thinks correctly about what happens during both periods and therefore reaches the right conclusion for the right reason. In mye experience, these people are very rare.
I claim that people trained to think about optimization are more likely to be the First Kind of Person than the Second.
Which kind of person are you?




People travel distances, not times. Let’s imagine a commute of 900 meters of walking, and 100 meters of escalator. Average walking speed is 1.4 m/s, but let’s pretend it is 1 m/s (as you say, the logic doesn’t change). And let’s pretend the escalator itself moves 1 m/s.
If the commuter never rests, they walk the 900 meters in 900 seconds, and travel the escalator in 50 seconds, for a 950 second commute.
If the commuter rests for 100 seconds on the escalator, they spend 900 seconds walking, and 100 seconds on the escalator, for a 1000 second commute.
If they rest for 100 seconds on the walking portion, they spend 1000 seconds there, and 50 seconds on the escalator, for a 1050 second commute.
This is more pronounced the more of the commute is “power-assisted rest”. At 500 yards of each, power-assisted rest for 500 seconds gives 500 seconds rest on a 1000 second commute, while resting without power-assist gives 500 seconds rest on a 1250 second commute.
Judging by “how far behind” Alice is may result in the right conclusion, but the reasoning is wrong. The correct reasoning is that power-assist can be applied to improve the efficiency of resting as well as to improve the efficiency of moving.
This is also why it’s more optimal to sleep on the bus than to sleep while walking to the bus stop.
Perhaps you are misunderstanding the meaning behind the statement that it is better to stand on the escalator because “at least you are moving”?
Walking up steps takes *effort*. The time resting on stairs does not spare you from even a single step. Rest as much as you like but all you do is exchange time for recovering some exhaustion, but if not exhausted then it is merely procrastination.
Time standing on the escalator spares you from having to take those steps – the longer you stand the fewer steps up you must take, thus “at least you are moving” indicates that you are sparing yourself the effort.
Don’t focus on travel times or distance traveled on an infinite escalator. I often find that humans tend to be more intuitively concerned with maximizing laziness.
Minimum travel time if they don’t rest is 15 mins.
If they each rest 1 min before going onto either stairs or escalator then travel time is 16 mins.
If Bob rests a minute after he enters the stairs journey time is 16 mins as he doesn’t move for first min.
If Alice rests for first min after getting on the escalator then after this minute she is someway up the escalator and so the rest of the journey takes less than 15 mins and so total time is faster than Bob’s 16mins and this is because she (unlike Bob) moved during her minute’s rest.
I therefore still believe that the intuition that resting while moving is better that resting while stationary is sound !
Edmond (#2):
Walking up steps takes *effort*. The time resting on stairs does not spare you from even a single step. Rest as much as you like but all you do is exchange time for recovering some exhaustion, but if not exhausted then it is merely procrastination.
Walking up steps takes effort. So does walking on the escalator. In fact, the effort expended is the same either way.
In fact, this is exactly what drives the (apparent) paradox. Walking up steps takes exactly the same effort as walking up the escalator. Walking up steps adds exactly as much to your progress as walking on the escalator. So how can it matter whether you walk on the steps or on the escalator?
S (#1):
If the commuter never rests, they walk the 900 meters in 900 seconds, and travel the escalator in 50 seconds, for a 950 second commute.
If the commuter rests for 100 seconds on the escalator, they spend 900 seconds walking, and 100 seconds on the escalator, for a 1000 second commute.
Yes, this is in fact key to the whole thing. If you walk on the escalator you spend less time on the escalator. That’s the often-overlooked “hidden cost” of walking on the escalator. (I claim both that this is the key to the whole thing and that any explanation that overlooks it is missing something crucial.)
It’s not clear to me whether you view your comment as agreeing or disagreeing with the thrust of the post. But as I read it, we’re in total agreement.
Rob Rawlings (#3): But I think your argument is more subtle than you’re giving it credit for.
Consider this variant:
Suppose Alice (on the escalator) and Bob (on the stairs) both spend their first minute walking. Then at the end of that minute, Alice is ahead of Bob so the remainder of her journey will be shorter than his. This proves that walking on the escalator is better than walking on the stairs. So if you’ve got to take a break, take it on the stairs!
That’s pretty close to your logic, and it leads to exactly the opposite conclusion. Now you’ve fleshed this out a little by referring to the minimum travel time, etc, but I contend that most people who give some version of your argument fail to include such details and therefore give an argument that is perfectly refuted by my twisted paraphrase.
I enjoyed this puzzle in your book, but I think you are too being harsh on the “local” solution here. It should almost always be possible to convert a “non-local” optimization problem into a “local” one by finding an appropriately invariant measure. In this case, relative progress in yards is a poor measure, since it changes across the stair/escalator transition. A better measure would be the relative lateness in minutes.
After her rest, resting-Alice reaches 20 yards at time 1.5, so she is only half a minute behind Alice. Resting-Bob, however, is a full minute late. And they will each stay that far behind across all modes of transportation. You don’t have to know how many floors of stairs and escalators lie ahead of them to predict that Alice will complete her journey half a minute late, while Bob will be a full minute late.
I wrote this up in Python: https://pastebin.com/2z0CxSWd
I think the results are right (15 minutes, 15.5 minutes, and 16 minutes).
Looking at the expressions for the two resting people, they’re identical except that resting_alice gets her escalator distance reduced for free. It seems reasonable to me to phrase that as “If you rest on the escalator, at least you’re making progress.”
This doesn’t apply to the infinite escalator because reducing infinity by a constant doesn’t have any effect, but in any other case that reduction would be the key difference.
Paul Grayson: Yes, I agree that it is much better to measure progress in time rather than distance. The fallacy, in essence, starts with the “observation” that a step on the escalator and a step on the stairs have exactly the same benefit, because they each get you the same number of yards closer to your goal. But this is wrong, because “steps closer” is the wrong measure; what matters is “time remaining”.
But (at least in my experience), the people who dismiss the problem as trivial are almost never doing so for that reason. They are perfectly happy to focus on distance and so end up saying things that can’t be right.
I agree with S(#1) and S(teve)(#5), the intuitive and correct explanation is: “The more time you spend on the escalator, the more you’re letting the escalator contribute to your progress, so if you’re going to rest somewhere, rest on the escalator.”
On the other hand, I think the real-world answer is close to what Edmond (#2) said — people want to minimize effort, not minimize travel times. In most of the kinds of places that have an escalator (airports, malls), you’re usually not in a hurry, but you’re also going to be doing a lot of walking and you want to conserve energy. A lot of people walk on the stairs portion and rest for the entire escalator ride, which suggests minimizing effort.
Edmond and Bennett have good points. The problem as framed ignores the cost of expending effort climbing the stair. If you add that as a variable, the whole problem changes.
Take an extreme case. Say walking one step is so onerous that you would be willing to arrive ten minutes later rather than take that one step. Then you have a corner solution: take as few steps as possible and ignore travel time.
If the problem had said that walking was costless and you should consider only travel time, then it would be pretty obvious that we are not modeling the average escalator user.
@Steve #6
An unsubtle version of my logic would be: Rest for a minute on the stairs and journey time is 16mins. Rest on the escalator for a min and your journey time is less than 16mins. The difference is entirely down to the progress you made while resting on the escalator compared to the lack of progress while resting on the stairs.
Both Bob and Alice have to walk up the stairs and this always takes 10 minutes. The only variables then is rest on the escalator or rest off the escalator and in all circumstances resting on the escalator is going to cut journey time as after the minutes rest they will have less distance left to travel.
It would be interesting to try and show that the “always rest on the fastest mode of transport” rule also applies to a journey consisting of multiple escalators of different speed.
BTW: I’m guessing I’m the Second Kind of Person – I just haven’t recognized it yet !
I think it’s important to include an analysis of the energy consumed during the trip. We are after all animals and it would be reasonable to assume we economize on energy spent not just time.
If we assume 1 energy unit per 1 yard of stairs (or escalator) then I’ve calculated the following:
Alice spends 15 minutes traveling 200 yards for a cost of 150 energy units.
Resting-Alice spends 15.5 minutes traveling 200 yards for a cost of 145 energy units. She “pays” half a minute to reduce her energy cost by 5 units.
Bob is the same as Alice.
Resting-Bob spends 16 minutes traveling 200 yards for a cost of 150 energy units. He “pays” a whole minute to not reduce his energy cost at all. This is a horrendous deal for Bob!
I like thinking about the corner conditions that Bennett and Zazooba have come up with. If you’re in an airport the only people in the airport walking up the escalator are those who are about to miss their flight, i.e. time is more important than energy saved. On the other hand, if you have no deadline and walking is extremely difficult (say you just had knee replacement surgery), then it makes sense to spend the extra time to take an escalator (or an elevator) even if the time spent is long (like an extra half hour).
Once you make the problem multivariate (time and energy) the intuition makes sense again.
After thinking about it a bit more, I think my above comment makes even more sense. If Resting-Alice is willing to “pay” half a minute to save 5 energy units, why wouldn’t she do this repeatedly? A whole minute for 10 energy units is on the same level. Pretty soon Resting-Alice is resting for the entire escalator trip. Since this is what most people are doing, I think I’m on the right track.
I’m sure a marginal analysis might come up with some reason each extra unit of time is more valuable, so at some point she might stop resting…
A cup of coffee and a moments thought indicates that on a multi-part journey where you have to slow down one of the legs by “resting” for a given period of time then it is always going to be optimal to “rest” on the fastest leg as this will have the least effect on total travel time on that leg. For example: if the escalator in Steve’s post took only one minute to complete its journey then resting on it for the whole minute would have relatively little effect on total travel time on the escalator – changing it by only a few seconds.
This now seems so obvious that I go back to my initial theory that this is Steve having some festive Fun !
dreum: I think it’s important to include an analysis of the energy consumed during the trip. We are after all animals and it would be reasonable to assume we economize on energy spent not just time.
No. The energy consumed by taking a step on the stairs is equal to the energy consumed by taking a step on the escalator, so we can ignore it. It’s certainly relevant to the question of whether Alice and Bob should rest, but not to the question of WHERE they should rest.
Zazooba:
The problem as framed ignores the cost of expending effort climbing the stair.
Yes, of course it does. That effort is the same on the escalator as it is on the stair, and so is irrelevant to the question of where you should rest.
dreum:
If Resting-Alice is willing to “pay” half a minute to save 5 energy units, why wouldn’t she do this repeatedly?
By the same argument, nobody who starts doing anything should ever stop. Maybe you should rethink this.
Zazooba wrote: Take an extreme case. Say walking one step is so onerous that you would be willing to arrive ten minutes later rather than take that one step. Then you have a corner solution: take as few steps as possible and ignore travel time.
Bingo. I really think it’s this simple. While economists are worried about local minima, the average Joe hates climbing stairs *a lot*. So he opts for the corner solution. Are we missing something?
coupon_clipper:
Say walking one step is so onerous that you would be willing to arrive ten minutes later rather than take that one step. Then you have a corner solution: take as few steps as possible and ignore travel time.
…
Are we missing something?
Yes, you’re missing the fact that if taking a step is so onerous you’re willing to arrive late in order to avoid it, you won’t walk on the stairs or the escalator. Surely there are such people, but those are not the people whose behavior we’re trying to explain.
This analysis is amusing, but it has little to do with why people stand still on escalators. People are lazy. They stand still to reduce the energy expended on the trip. Resting-Alice expends less energy than the alternatives. Her supposedly fallacious reasoning actually gets her correctly to this conclusion.
Steve’s analysis is more complicated because he assumes that the goal is to minimize average speed, instead of energy expended. Speed is distance divided by time. Speed is linear in distance, so strategies involving varying distance are intuitive enough. Speed is nonlinear in time, so strategies that vary time are a little more subtle.
Nevertheless, it is intuitively plausible that a strategy that involves standing stationary is not the best way to maximize your average speed. And that reasoning works fine in this case.
“Now for many many optimization problems, the key is to focus in on the local effects.”
If your goal is minimizing expended energy, you stand on the escalator. If your goal is minimizing trip time, you walk steadily. Focusing on the local effects works fine in both cases. But you are not really doing either here. You are comparing the average speeds of Resting-Alice and Resting Bob, as some sort of lesson in how speed is nonlinear in time.
SL: “There are two kinds of people in this world: The first kind wonders why people stand still on escalators but not on stairs. The second kind wonders what’s wrong with the first kind…
Third Kind of Person, who thinks correctly about what happens during both periods and therefore reaches the right conclusion for the right reason.”
The fourth kind is the one who rides the escalator in order to
climb the Stairmaster on the second floor spa, at the shopping mall.
And the fifth kind – me – who always climbs the stairs, being aware that fat kills, and exercise is never a bad thing, appalled at watching a nation devolve into a pack of slugs, mindlessly pushing buttons to open doors, thanks to the 1990 Retarded Americans Act. Which isn’t germane to this economics quiz, but definitely relates to economics.
SL wrote: “Yes, you’re missing the fact that if taking a step is so onerous you’re willing to arrive late in order to avoid it, you won’t walk on the stairs or the escalator. Surely there are such people, but those are not the people whose behavior we’re trying to explain.”
Got it!
IOW, the lazy people who climb zero steps on the escalator are not part of the puzzle. The puzzle is to explain the people who take *some* steps on the escalator and rest part of the time on the escalator, but don’t rest at all on the steps.
Thanks for explaining, Steve.
coupon_clipper (#24): Yes, exactly.
Roger Schlafly (#22):
People are lazy. They stand still to reduce the energy expended on the trip.
No, you’ve missed the point entirely. To reiterate what I’ve said in other comment responses above: A step on the stairs requires exactly the same energy as a step on the escalator, so that energy expenditure cannot be relevant to why people are willing to take that step on the escalator and not on the stairs.
Steve Landsburg (#4):
Walking up steps contributes the same to the journey as walking up escalators, but standing on stairs contributes nothing to the journey while standing on the escalators does (for at least you are moving).
That it takes the same effort to take a step on the stairs as it does on the escalator is not relevant, for the pertinent period is the standing not the stepping.
Given a stairway of 100 steps:
Bob on the stairs expends 100 steps to complete the journey to the top.
Resting-Bob… still expends 100 steps to get there.
Resting on the stairs spares himself not a single step.
Resting on the stairs has no value.
Alice on the escalator expends 50 steps to complete the journey to the top.
Resting-Alice expends only a few steps or likely none at all, yet still gets to the top.
Resting on the escalator is worth up to 50 steps.
“energy expenditure cannot be relevant to why people are willing to take that step on the escalator and not on the stairs.”
As Edmond explains, resting on the escalator reduces the energy expended for the trip, while resting on the stairs does not.
In Steve’s original example, Resting-Alice expends less energy (ie, takes fewer steps) than Alice, Bob, or Resting-Bob. Resting-Alice walks for 14.5 min, while Alice, Bob, and Resting-Bob each walk for 15 min. Thus Resting-Alice is simply deciding to save 30 seconds of walking, compared to those alternatives.
Resting on the escalator is faster than resting on the stairs, we get this right if we’re careful with the arithmetic. If I was less lazy I’d try to work this out with algebra and I suspect it would be a second order effect (in some natural variable).
Turns out a lot of us who’re not in the mood to think carefully about the problem get the right answer for bad reasons.
If we’re trying to explain the behaviour of actual people, we know empirically that most are not doing the calculation correctly (we’ve sampled people trying this by literally asking them, that’s kinda the point of the post). Which means the right answer to “why do people rest on the escalator” probably isn’t “We’ve figured out this is more efficient” so much as “We’ve guessed this is more efficient for the wrong reason” or even “I like the feeling of progress/ I really dislike the feeling of being completely stationary”.
Roger:
1) The cost of taking a step is energy expenditure. The benefit of taking a step is progress toward your goal.
2) We are trying to explain why Benefit(Escalator)-Cost(Escalator) is greater than Benefit(Stairs)-Cost(Stairs)
3) Because Cost(Escalator)=Cost(Stairs), this is equivalent to explaining why Benefit(Escalator)>Benefit(Stairs).
4) Your argument, unless I greatly misunderstand it, is that the reason Benefit(Escalator)-Cost(Escalator) > Benefit(Stairs)-Cost(Stairs) is that Benefit(Escalator)>Cost(Escalator)=Cost(Stairs)>Benefit(Stairs), or at least that this is possible. But your argument for why it is possible starts from the assertion that Benefit(Escalator)>Cost(Escalator), which is what we were trying to prove in the first place. So your argument contributes nothing.
The intuitive conclusion for neurotypicals is “If you’re going to spend some time resting, and your path of travel involves an escalator, it’s better to rest on the escalator.” We wish to reach this conclusion for sound reasons rather than unsound ones.
It’s easier for me to see that by reformulating the problem like this:
Assume there is nothing but a single escalator between you and your destination.
Scenario 1: You step on the escalator and rest for one minute. Then you start walking continuously to the top. While you rest for one minute you progress 10 yards, and then you cover the remaining 90 yards in 4.5 minutes, for a total travel time of 5.5 minutes.
Scenario 2: Before you step on the escalator, you rest for one minute (possibly creating an obstacle for other travelers, but for simplicity’s sake let’s act like a cartoonish caricature of an economist and ignore any negative externalities*). That’s one minute making zero progress, and then five minutes walking up the escalator, for a total time of 6 minutes. This takes more time (and more energy expenditure).
Is there anything important that this simplified problem does not capture?
*Although for the sake of fun, I’ll work through that one too: If the person behind you is a continuous walker who would normally have taken 5 minutes to go up the escalator, you would add 1 minute to their travel time by taking your rest at the bottom of the escalator, but only 30 seconds if you had rested while riding. If the other person would have preferred to rest for a minute while riding (normally spending 5.5 minutes total), well, they have now gotten their one-minute rest waiting behind you at the bottom and can justify walking up continuously for 5 minutes for a total of 6 minutes. Assuming you are the only weirdo who likes to rest at the bottom and the rest of the world is split into minute-resters and no-resters, you cost both those kinds of people an additional 30 seconds of total time, all of which is accounted for by and additional 30 seconds of energy-intensive climbing. So you are being equally rude to everybody (assuming a preference for a certain amount of resting time implies nothing about a preference for less total energy expenditure…)
3) Because Cost(Escalator)=Cost(Stairs), this is equivalent to explaining why Benefit(Escalator)=Cost(Escalator)
I don’t this is correct.
If you’re goal is to get somewhere (i.e. the Xth floor), it’s costlier to walk on escalators because you’re expending energy to acquire a benefit that you would get if you’d have never taken a single step. It’s less costly to walk on stairs.
Really? You are trying to prove Benefit(Escalator)>Cost(Escalator)? An escalator is a machine that takes you where you are going. What is not to like about that?
Kyle makes a good point. If you want a local justification for Resting-Alice, just compared standing for a minute just before getting onto the escalator, to standing just after. The local analysis says that it obviously better to let the escalator engines do some work for her.
Roger (#33):
You are trying to prove Benefit(Escalator)>Cost(Escalator)?
No. I am OBSERVING that some people stand still on escalators and walk on stairs. For those people, Benefit(Escalator)-Cost(Escalator)>0>Benefit(Stairs)-Cost(Stairs). But I also know that Cost(Escalator)=Cost(Stairs). Therefore I am concluding that Benefit(Escalator) > Benefit(Stairs). And I am asking how to reconcile this with the observation that Benefit(Elevator) and Benefit(Stairs) appear to be equal if one does the obvious local calculation.
As for escalators being good, that was of course never at issue.
(Is it possible that you were misreading Benefit(Escalator) to mean something like the benefit of having an escalator? That would be an entirely irrelevant variable, since we are taking the existence of the escalator as given. Benefit(Escalator) means “benefit of taking a step on the escalator”.)
Z(#32): The passage you’re quoting contained a typo which is now fixed, and which I think might have confused you. My apologies.
Kyle (#31):
Yes, your reformulation of the problem is fine: Should I take my rest as soon as I get on the escalator, or just before?
Your calculation (call it KYLE) shows correctly that it is better to rest on the escalator. But it does not answer the question.
Here is why: Every step I fail to take leaves me one step farther from my goal than I could have been. This seems to imply that choosing not to step during the pre-boarding minute is exactly as costly as choosing not to step during the post-boarding minute. So it doesn’t matter where I take my rest. Call that argument ANTI-KYLE.
The question is: What is wrong with the ANTI-KYLE argument? Presenting the perfectly correct KYLE argument does not answer that question.
The answer is that the ANTI-KYLE calculation fails to correct for the fact that if you rest on the escalator, you end up getting to spend more time on the escalator. The KYLE argument implicitly accounts for that; the question is “What, precisely is the KYLE argument accounting for that the ANTI-KYLE argument is missing”, and “Spending more time on the escalator” is the answer.
Steve say ‘the resolution of the problem has nothing to do with what happens while you’re resting’
But the only variable that matters to answer the question of whether it is better to be resting-Alice or resting-Bob is the speed at which Alice and Bob travel while resting.
Rob Rawlings:
The only variable that matters to answer the question of whether it is better to be resting-Alice or resting-Bob is the speed at which Alice and Bob travel while resting.
Here is why I think this is misleading:
If you’re deciding whether or not to rest, the right question is not “What speed do I travel while resting?”. Instead, the right question is “How much speed do I *sacrifice* by resting?” Alice’s answer is: I sacrifice 10 yards per minute (because resting reduces my speed from 20 to 10); Bob’s is: I sacrifice 10 yards per minute (because resting reduces my speed from 10 to 0). Same answer, so we’ve failed to point to an important difference between Alice and Bob.
Again, speed while resting cannot be the issue. If you ask me whether I want to rest, and tell me that my speed while resting will be 30mph, I have no basis to make a decision. I need to know “How fast would I be going if I *didn’t* rest?” It’s only the difference that matters. And for Alice, that difference is the same as it is for Bob, which means we have to dig deeper to find out why one rests and the other doesn’t.
Steve, I’m with Edmond. Suppose you’re a lazy person who wants to reach your destination, but wants to minimize the effort expended in doing so. Then when confronted with a staircase, you will walk up the staircase, because that’s the only way to get to your destination. But when confronted with an escalator, you will stand still on the escalator, because that will still get you to your destination while expending less effort compared to walking on the escalator.
What is wrong with my reasoning?
Keshav, here’s what I said above. I think this will clear it up: “the lazy people who climb zero steps on the escalator are not part of the puzzle. The puzzle is to explain the people who take *some* steps on the escalator and rest part of the time on the escalator, but don’t rest at all on the steps.”
The escaloator is a moving STAIRWAY.
Stairs, to be safe, need a maximum rise rate of aobut 8″.
Escalators can, and do, have a greater rise to them, since they are not designed for walking (climbing).
quote:
RISE: the height of one step in a staircase. This is the amount of vertical distance one moves when stepping from one stair onto the next. The rise should be between 5″ & 7.5″ with the ideal rise for a residence being 7″.
https://inspectusa.com/rise_run_stringer_stairs_calculator.php
Steve,
The question we are trying to address is “whether it is better to be resting-Alice or resting-Bob in terms of total journey time”. Is that correct ?
if so, then I’m missing why ‘How much speed do I *sacrifice* by resting?’ is more Important than ‘How much journey time do I add by resting’. The answer to the first question is always ‘I sacrifice the speed at which I walk’, while the latter depends on both the speed I walk and the speed I travel when resting and its only when we know these things that we can answer the question.
Even looking at things your way, where the key things is the catch-up period when people are switching from the stairs to the escalator or vice-versa then it is the relative speeds of the stairs and escalators that (resting and non-resting) Bob and Alice happen to be on during the catch-up period that determines that it does actually make more sense to be Resting-Alice. Just knowing ‘How much speed do I *sacrifice* by resting?’ is no help at all in determining that.
I did not get from your post that we were trying to answer the question of ‘why one rests and the other doesn’t’. But surely if we were then it would still be more useful to know ‘resting on the stairs adds 1 min to journey time , resting on the escalator adds 30 secs’ than to know ‘resting slows you down by 10 yards a minute’.
Bob Rawlings,
I believe you are correct. Since the goal is time saved, the fact that speed sacrificed is the same is not relevant. Speed is distance over time, but what is relevant is the inverse, that is time over distance. You sacrifice less time over distance resting on the escalator because you stay moving, just at half the speed. The same problem arises in measuring fuel efficiency of automobiles. The correct measure is gallons per mile, not miles per gallon, because gallons is what you’re trying to save. Mpg is the inverse of the right measure.
@coupon_clipper If Steve shares your view that “the lazy people who climb zero steps on the escalator are not part of the puzzle”, then I’d like him to confirm that. Otherwise I’d like to see what his response is to my comment #39.
‘If you’re deciding whether or not to rest, the right question is not “What speed do I travel while resting?”. Instead, the right question is “How much speed do I *sacrifice* by resting?” ‘
I would say rather that ‘what percentage of non-resting speed do I sacrifice by resting’ is a better question. If resting reduces my speed from 1000mph to 995mph the cost is much lower than if it was reduced from 6mph to 1mph. The benefits of rest (reduced effort) are presumably the same in either case.
Whether you rest for a minute on the stairs on rest for a minute on the escalator you end up a minutes walking time behind someone who does not rest. To look at it Steve’s way this is because you have in both cases sacrifice 10 yards per minute for a full minute.
However basic math also tells us that resting on the stairs for a minute costs one minute in journey time, while resting on the escalator costs only 30 seconds.
So we have to conclude the the costs of sacrificing 10 yards per minute for a minute varies depending on the underlying speed. The costs is one full minute on the stairs, 30 seconds on the elevator and would be close to zero on an elevator moving at the speed of light.
The answer seems to distill to:
When you walk a step on an escalator, you are expending energy to make a step of progress the escalator would have made for you, if you hadn’t walked. You are sacrificing a benefit that would have been free.
On the other hand, when you walk a step on the stairs, you sacrifice nothing. The stairs don’t give you free progress.
The answer to “Why do people walk less on the escalator?” is the same as the answer to, “Why do people work less when their welfare benefits are clawed back by the income they earn?”
@Phil “When you walk a step on an escalator, you are expending energy to make a step of progress the escalator would have made for you, if you hadn’t walked. You are sacrificing a benefit that would have been free.” Yes, exactly. I don’t know what problem Steve sees in this reasoning.
Steve,
This is awesome; I read this and pondered on the plane when my phone was on “airplane mode.” It was good fodder for the whole flight.
Before I dive into this, let me ask a clarifying question: Before, when I wrote my (gentle) critique of your Slate analysis, my biggest problem was that you were saying the key was to analyze in terms of time rather than distance. Back then, I didn’t think that distinction was what was driving things.
Now it seems you also are focusing on something else, and agree that whether you measure progress by distance or time, the actual solution is still expressible?
(I’m not asking so I can run victory laps, I just want to see if you agree that your own focus has shifted.)
Keshav/48: Why do you think Steve has a problem with that reasoning? I posted under the assumption that he’d agree with it, that I was just reframing his answer.
Where you rest is easy: You always rest on the fastest leg of your journey
Whether you rest is harder: You rest if the utility of rest is greater than the dis-utility of a longer journey time (a function of both walking speed and underlying speed).
@Phil The entire thrust of Steve’s post is that people who say “at least you’re making progress” are arriving at the right answer for the wrong reason. Whereas you seem to be saying that the “at least you’re making progress” reasoning is valid. Am I reading you wrong?
Also, can you tell me if you agree or disagree with my comment #39?
Keshav/52: Your #39 explains why lazy people (energy minimizers) always walk on the stairs and never walk on the escalator.
But it doesn’t explain why, when people DO choose to walk on the escalator, they also choose to do their “non-walking” on the escalator rather than the stairs.
Keshav/52: By choosing to stand still on the escalator rather than the stairs, you maximize your progress *for the same amount of energy expenditure*.
My explanation doesn’t require me to know people’s tradeoffs between energy and progress. It just requires the assumption that, for equal amounts of energy, they prefer to make more progress.
It’s like, I don’t have to assume that for their dollar, people prefer five apples to four oranges. I just need to assume that, for the same dollar, they prefer five apples to four apples.
What’s wrong with this argument:
It clearly doesn’t matter which order you do stairs or escalator, so assume both do stairs first. It clearly doesn’t matter which stair you rest on, so assume Bob rests on the last stair just before joining escalator. Let’s also say Alice rests as soon as she steps on the escalator.
Now it’s obvious that Alice and Bob reach the escalator at the same time; Alice travels some distance in the next minute while Bob doesn’t; and after that they go at same pace so Bob can never catch up.
Doesn’t this suggest that the difference *is* simply due to the fact that Alice is moving while resting?
The way you give the problem so that they do stairs and escalator in different order just adds an unnecessary complication by making it harder to compare their relative progress.
“The puzzle is to explain the people who take *some* steps on the escalator … but don’t rest at all on the steps.” [40]
That person is not optimizing time or average speed or energy expended. Nobody has explained what she might be optimizing. If that is the puzzle, it is unsolved.
If the purpose is to compare to some alternative, Eric [55] explains it nicely. The naive explanation that moving is better than not moving turns out to be correct.
Roger Schlafly (#56):
That person is not optimizing time or average speed or energy expended. Nobody has explained what she might be optimizing. If that is the puzzle, it is unsolved.
On the contrary, the whole point of this post is to explain that, despite the obvious (but fallacious) argument to the contrary, this person *can* be optimizing an objective function that counts time saved as a benefit and energy expended as a cost. When you say “nobody has explained” this, I don’t know whether you mean that you didn’t read the post or that you think that the explanation in the post is incorrect.
Eric (#55):
I very much like your reformulation: They both take the stairs first, then Bob rests at the top of the stairs while Alice rests on the escalator, then Bob joins the escalator and is permanently behind Alice.
You say this shows that the key is that Alice gets to move while resting.
I’d prefer to say that it shows that the key is that Alice spends more time on the escalator.
Let me start by conceding that your interpretation is pretty convincing. But I think it still fails to answer this question: If you rest, you lose 10 yards of progress for every second that you rest. This is true whether you rest on the escalator or whether you rest on the stairs. So how can it matter where you rest?
Your interpretation makes it very clear that it does matter, and does pretty convincingly seem to lay the blame at the feet of the fact that Alice moves while resting. But I think it still fails to answer the boldfaced question.
On the other hand, your exact reformulated story matches just as well with an interpretation where it’s “Alice’s extra time on the escalator” that matters.
In brief: I think you’ve convinced me that yours is a fairer and simpler setup, and that it makes it crystal clear what the right answer is. But I also think that your interpretation of that setup fails to answer the boldfaced question. (I will think more on this, though.)
Bob Murphy: I believe the rephrasing in terms of time is (not entirely trivially) equivalent to the story I’m telling here, but am hoping that this version of the story is easier to follow.
I also realize that I have not spelled out why I believe that the “measure benefits in terms of time” story and the “Alice spends more time on the escalator” story are in fact exactly the same story, though one of them is wearing a disguise. If I find the enregy, I’ll write this up.
‘If you rest, you lose 10 yards of progress for every second that you rest. This is true whether you rest on the escalator or whether you rest on the stairs. So how can it matter where you rest?’
(I think you mean minute not second).
Go back to your original setup where Bob takes the stairs first and Alice the elevator. Both rest on the first step.
Take a snapshot after 1 minute.
Both are 10 yards behind where they would be without the rest.
Bob is at the bottom of the stairs and Alice is 10 yards up the elevator.
For the rest of the journey Bob stays 10 yards behind Alice.
Bob’s total journey time is 16 mins. He spends 6 mins on the stairs and 5 mins on the escalator.
Alice’s total journey time is 15.5 mins. She spends 5 mins on the stairs and 5.5 mins on the escalator.
But all the damage is done in the first minute. Alice has less distance left to travel so arrives sooner. The fact that Alice ultimately spends more time on the escalator seems irreverent.
In fact after that first decisive minute Bob (5 mins) has more escalator time than Alice (4.5 mins). It is the fact that spent the first minute on the faster mode of transit that wins the day.
To my mind this means that it is the “traveling while resting” argument that trumps the “more time on the elevator” argument.
‘For the rest of the journey Bob stays 10 yards behind Alice.’
That is wrong. Because Bob spends longer on the escalator for the rest of the journey he actually catches up 5 yards and 30 seconds.
@61
No. When Alice exits the elevator she is 10 yards ahead, which Bob makes up in 30 seconds.
@62
I totally messed up the timings so making my point very confused.!
The relative distances are actually quite complex.
Alice will be 10 yards ahead after 1 min, she will increase her lead during the time she is walking on the escalator and Bob walking on the stairs. When she is at the top she will be 55 yards ahead as Bob is only 45 yards up the stairs by then. For the next 5.5 mins they are both walking on the stairs so the gap stays 55 yards. Then for the next 4.5 mins Bob catches up until minute 10.5 when Alice finishes with Bob 10 yards behind which it takes him 30 seconds to complete.
Your way of looking at things where they both do the stairs first with one then resting on the last step of the stairs and one on the first step of the escalator is indeed way simpler and better !
Resting is in effect making your journey longer. If you walk at 10yards/minute then resting for a minute is the same as adding 10 yards to the leg of the journey where you rest.
So the answer to the question ‘how can it matter where you rest?’ is that it maters because in some locations you will make up the added yards faster than in others. In this case you make up the added yards in 30 seconds on an escalator and 1 minute on the stairs.
Here is another argument for standing on an escalator:
Tokyo … launched a campaign this month calling on riders to stand on both sides of the escalators inside some of the city’s busiest transit hubs.
Signs are posted on walls and above escalators, reading, in both Japanese and English, “Walking on escalators may lead to accidents caused by collisions or luggage.” Bright pink handrails carry similar messages. And in some stations, security staff with neon-colored vests stand watch and guide people. If people are really in a hurry, JR East suggests, they should take the stairs.
Consider an alternate version of this question:
Suppose you have a set of stairs, and an escalator running parallel to the stairs, up some large incline.
Anybody can switch at any point between the stairs and the escalator (let’s ignore the tripping hazard), and the only limitation is that nobody is allowed to be on the escalator for longer than 60 seconds, total (whether you are standing or moving), and this is enforced by some eye in the sky that levies fines if you break the rules. Assume that the incline is large enough that you cannot get all the way up in 60 seconds on the escalator (unless you are practically sprinting on the escalator), so almost everybody is going to have to take some combination of the stairs and the escalator, and almost everybody is going to have to rest at some point.
Now you really do have a situation where it makes zero sense to rest on the escalator as opposed to the stairs. All that matters is that you use up all of your allotted 60 seconds on the escalator; other than that, resting on the stairs vs. the escalator does not change your total travel time or the number of steps you have to take.
And yet, my intuition says that most people would still choose to rest during their allotted time on the escalator, based on the fallacy that “at least I’m still getting somewhere”. I feel like I’d be strongly drawn to doing this myself, even knowing that it made no sense.
I suspect there are monetary analogs of this in the real world. There may be scenarios where someone has a given fixed income for part of the year, but it’s not enough to live on year-round, so they have to work for part of the year. And, I’ll bet a lot of them decide to work during the time periods that their fixed income is not coming in, even though the end result is exactly the same as if they did the work and earned the passive income at the same time.
Thanks for another fun brainteaser.