 The Intelligent Design folk tell you that complexity requires a designer.
The Intelligent Design folk tell you that complexity requires a designer.
The Richard Dawkins crowd tell you that complexity must evolve from simplicity.
I claim they’re both wrong, because the natural numbers, together with the operations of arithmetic, are fantastically complex, but were neither created nor evolved.
I’ve made this argument multiple times, in The Big Questions, on this blog, and elsewhere. Today, I aim to explain a little more deeply why I say that the natural numbers are fantastically complex.
Here’s one way to think about simplicity versus complexity: Simple things have short descriptions; complex things have only long descriptions. A string of a million zeros is very simple because I can describe it in six words: “A string of a million zeros”. A string of a million random numbers is complex, because it takes a long time to describe all of the content.
Now what about the system of natural numbers? To first appearances, there’s a very simple description: Start with 0, then add 1, then add 1 again, keep doing this forever, and those are the natural numbers. Unfortunately, “keep doing this forever” is a little vague, and the complexity comes in when you try to make that precise.
So if you were setting out to give a complete description of the natural numbers, where would you start? Probably here:
- We have a number called zero, and then every number has a successor.
But that description fits a lot of things besides the natural numbers; it also fits, for example, the integers (the integers, unlike the natural numbers, include negatives). Here’s an attempt to fix that:
- We have a number called zero, and then every number has a successor, and zero is not the successor of any number.
Better, but still no good; this fails to rule out a system where 1 follows 0, 2 follows 1, 3 follows 2, and 1 follows 3, like this:
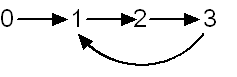
To fix that, we have to add a clause specifying that no two numbers (such as 0 and 3) have the same successor. But even now, we’ve only just begun.
We still haven’t ruled out the possibility of infinite gaps between numbers. For all we can tell from our description so far, the number system might look like this:
![]()
with infinitely many numbers in between 3 and that very large number N. How can we rule that out?
This one is not so easy. We’d like to say that all gaps between numbers are finite. But how do we define “finite”? Usually we say a number is finite if it’s part of the set of natural numbers. Or to put this another way: We’d like to say that no matter where you start (say at N), you can’t count backward forever; eventually you’ve got to hit a stopping point. But what does it mean to count backwards forever? It means counting back more than a natural number of steps. There’s that circularity again.
What we really really need, it turns out, is to add a clause like this to our description:
- Every non-empty subset of the natural numbers has a smallest element.
This will solve our problem, because it implies, for example, that the set of numbers you can reach by counting backwards from N has a smallest element—eliminating the possibility of that infinite gap.
But this assumption, stated in this way, opens a can of worms that almost nobody wants to open. Here’s why: For the first time, we’ve been forced to talk about sets of natural numbers, as opposed to natural numbers themselves—and even to talk about all those sets at once. In technical jargon, we’ve left the world of first-order logic and entered the world of second-order logic. But that’s a very strange world indeed. In ordinary (first-order) logic, we have a small number of rules of inference that allow us to proceed, for example, from “Socrates is a man” and “All men are mortal” to “Socrates is mortal”. But in second-order logic, not only are the rules of inference not finite; they cannot even be printed out (even in an infinite amount of time) by any computer. That’s why the great logician Willard van Ormand Quine insisted that second order logic is not logic, and why mathematicians usually prefer to avoid it.
All is not lost, though. Instead of adding one second-order axiom, we can add infinitely many first-order axioms, viz:
- The set of odd numbers has a smallest element.
- The set of numbers greater than 7 has a smallest element.
- The set of numbers that can be reached by counting backward from 100 has a smallest element.
And so on.
Okay, our description of the natural numbers just got infinitely long, but at least it’s infinitely long in a simple sort of way. We’ve added an infinite number of axioms, but they all fit the same simple pattern—a pattern that you could easily train your computer to recognize.
Unfortunately, though, we still have a long way to go to get to a full description of arithmetic. First, we have to add rules for addition and multiplication. (If we don’t do this, then we won’t be able to talk about interesting subjects like prime numbers.) Now we’ll want to add even more axioms. But now we come up against the content of Godel’s incompleteness theorem: NO description suffices. No matter what axioms you add, your description will always fail to distinguish the natural numbers from any of an infinite number of other structures. (Those other structures are usually called “non-standard models of arithmetic”).
When I say that “NO description suffices”, you might reasonably ask what counts as a description. Here’s what counts: A description is some (possibly infinite) list of axioms that some computer program is capable of recognizing. So if, for example, you try to describe arithmetic by listing every true statement about it, I will cry foul, because no computer program is capable of recognizing every true statement about arithmetic. (This is not just an observation about the state of the art in computer programming. It is a theorem about all possible computer programs.)
That’s the sense in which arithmetic is fantastically complex. Not only do the natural numbers have no finite description; they have no description that is recognizable by any computer. If “simple” means “capable of a short description”, then the natural numbers are about as far from simple as you can get. Not only do they have no short description, they don’t even have an infinite description.
Other mathematical structures are simpler. Euclidean geometry, for example, can be fully described by a first-order theory, and there is a computer program that can distinguish true from false statements in that theory.
Likewise for the (first-order) theory of the real numbers. There are axioms for the real numbers that suffice to prove all true first-order statements about the real numbers, and there is a computer program that can distinguish the true statements from the false. In that sense, the real numbers are far simpler than the natural numbers. (There are still non-standard models of the real numbers, but through a first-order lens, they are indistinguishable from the real thing.)
(You might be tempted to think that because the natural numbers sit inside the real numbers, they must be simpler. But of course any sequence of arbitrary complexity sits inside the very simple sequence 010101010101….., if you can pick and choose what to keep and what to throw away. Complexity can reside quite comfortably inside simplicity.)
Did that help?



What about Conway numbers?
Firstly, pure entropy as in the heat death of the universe, is more complex than what you are referring to as complexity. You mean “order” or possibly “complex order”, which is a difficult concept at best.
Secondly, I hope no-one at all would claim that order requires either evolution or a designer. The pebbles of the sea sort themselves by size without design and without evolution.
Thirdly, numbers don’t “exist” in the same sense as platypuses exist, i.e as concrete objects in the real world, so they don’t require the same sort of explanation.
Trick question! No, it didn’t help … and if it did (in the sense of having reduced how much more help I need), that would’ve contradicted Godel, right? ;-)
“The pebbles of the sea sort themselves by size without design and without evolution.”
This sort of sorting is, however, basically a “ratchet” mechanism, which is not unlike natural selection in a way: it’s a set of rules in which a particular sort of movement is preserved/selected for in what is otherwise pretty random motion.
How do your axioms exclude the infinite (ordinal) numbers? I think you have to say that the minimum has to be finite, since any set of (countable) ordinals has a (possibly infinite) minimum.
Would it be correct to say that the conclusion of this post is that Peano arithmetic has infinite Kolmogorov complexity? I think not, since Peano arithmetic consists of the Peano axioms, which have finite K.complexity. But then, how to put it, other than: “the natural numbers have infinite K.complexity”? The problem is that the natural numbers are an intuitive concept, so that’s saying that some intuitions cannot be described with any finite number of words. (But with the advantage of having proved it mathematically.)
A related issue: how do you define “non-standard” arithmetic? since there cannot be any finite definition of standard arithmetic, the distinction between standard and non-standard seems to be based on intuition.
This post raises other issues as well, but I mean it in a positive sense: it makes me aware of how much I don’t know; it turns unknown unknowns into known unknowns.
For instance: second-order logic, as I understand from this post, also has infinite K.complexity; and uncountably infinite, at that. How does that compare to the K.complexity of the natural numbers? is the K.complexity of the natural numbers the smallest infinite K.complexity? (just like the cardinality of the natural numbers is the smallest infinite cardinality.)
@Snorri_Godhi: Steve_Landsburg didn’t tell you, but I have been making roughly the same point here, which is a big part of what led him to make this post.
Additionally, arithmetic must be simple, or else there would be no point to using it in scientific theories, which are ultimately trying to compress the data in our observations. Using something infinitely complex would defeat the purpose.
Snorri (and Silas): Peano arithmetic is not arithmetic. The existence of non-standard models (which satisfy the Peano axioms but which are not arithmetic) tells you that. My whole point here is that to describe *arithmetic* is far more difficult than to describe *Peano arithmetic*.
(Edited to add): Snorri, on rereading your comment, I see that you already understood this.
Snorri: The standard model is distinguished (within any given model of set theory, at least) by the condition that all models contain it as an initial segment.
Silas: You said (both here and on your own blog, and repeatedly):
arithmetic must be simple
You’ve also said repeatedly that simplicity, in this context, should be understood as having a short description. Now there are theorems galore saying that arithmetic has no short, or even finite, or even computable, description. Apparently you doubt those theorems, or have never heard of them, or refuse to think about them, or something. Okay, then, fine. Keeping in mind that a description is not a description unless it specifies a structure uniquely, what is your short description of arithmetic?
Steve:
The standard model is distinguished (within any given model of set theory, at least) by the condition that all models contain it as an initial segment.
Am I correct to infer that all non-standard models have finite K.complexity?
If so, this also seems to address the worry expressed in my first paragraph: the natural numbers are not just an intuitive notion: they are the unique model of Peano arithmetic that has infinite K.complexity. There might be a paradox, though, because I have just defined the natural numbers with a finite number of words.
I have skipped through the debate on Silas’ blog and I am uneasy with the use of the word “true”. As we previously agreed in this blog, the “true but unprovable” statements are true only if arithmetic is consistent (which is unprovable). Alternatively, they are true of the natural numbers, or of the standard model of arithmetic; but again, I am not sure that the standard model can be specified except by intuition.
Snorri: No model of arithmetic, standard or non-standard, can be specified in a computable way. In fact, in the non-standard models, you can’t even *define* addition and multiplication in a computable way.
Snorri:
I didn’t understand the claim that the (standard) natural numbers is the unique model of PA which has finite descriptive complexity. The standard theorems (in Chapter 25 of Computability and Logic, Edition 5, by Boolos, Burgess, and Jeffrey, for instance) is that the order-properties of any countable non-standard model of PA are uniquely determined. More specifically, every countable nonstandard model of PA looks like the nonnegative rationals with 0 replaced by a copy of the naturals, and every rational replaced by a copy of the integers. But … the definition of addition and multiplication can be anything whatsoever (subject to the proviso that you still end up with a model of PA!). In fact, there can be no countable non-standard model of PA in which the operations of addition and multiplication are recursive! More specifically, no matter what recursive encoding of the elements of the non-standard model you come up with, you cannot code up addition and multiplication as relation representable in PA (in terms of that coding).
So it is not clear that non-standard models of PA are of finite K. complexity! Unless I am way off in my understanding of what you mean by K. complexity!
No model of arithmetic, standard or non-standard, can be specified in a computable way.
In this case, you are getting into a blind alley — or perhaps in a loop, because all you are saying is that a model that cannot be specified in a computable way has infinite K.complexity. The only way out that I see is for you to specify it in a non-computable way, which so far you have shied away from doing. (And the non-computable specification must still be specific enough for you to prove that it is non-computable.)
Suresh: thank you for the reference.
Snorri: Kolmogorov Complexity is a concept that applies to strings of bits, not to mathematical objects. So it is a bit of an abuse of language to keep talking about the “K complexity of arithmetic”. What I am claiming is that arithmetic is very complex in a sense that is closely *analogous* to the notion of K. complexity. That’s the first thing.
The second thing is that you keep referring to “infinite” K-complexity, but one of the key points here is that things are far worse than infinite; they’re not even computable.
Any model of arithmetic requires a non-computable set of statements to distinguish it from all other models. In that sense, models of arithmetic are highly complex according to a standard which is very close in spirit to K-complexity, though the precise notion of K-complexity does not exactly apply here.
In standard arithmetic, it’s at least possible to *define* addition and multiplication in a computable (more precisely: recursive) way; in non-standard models, not even that is possible. But that’s a tangential issue. The key point is this: Standard arithmetic cannot be uniquely described (that is, described in a way that differentiates it from non-standard models) without giving a *non-computable* (not just infinite) amount of information.
Where to start? in this comment, I shall [attempt to] deconstruct your latest; later on, perhaps tomorrow (it’s past 11pm here, and there is a sale of Islay whisky going on), I might try to go back to 1st principles.
Kolmogorov Complexity is a concept that applies to strings of bits, not to mathematical objects.
I am uneasy with your distinction between strings of bits and mathematical objects, especially when you identify physical and biological objects with strings of numbers; but let’s skip this if you don’t mind.
So it is a bit of an abuse of language to keep talking about the “K complexity of arithmetic”. What I am claiming is that arithmetic is very complex in a sense that is closely *analogous* to the notion of K. complexity. That’s the first thing.
OK, that’s fine, pace Silas Barta there are several definitions of complexity; e.g. there is computational complexity, which has nothing to do with K.complexity. But you need to make your notion of complexity measurable before you can argue that standard arithmetic is “very complex”.
The second thing is that you keep referring to “infinite” K-complexity, but one of the key points here is that things are far worse than infinite; they’re not even computable.
Here is the sticking point: an infinite string of bits has infinite K.complexity (in fact, “almost all” infinite strings of bits have infinite K.complexity) AND it is not computable. Hence, non-computability looks no worse to me than infinite K.complexity.
That is the main problem that I have with your latest comment; but I also take issue with the following:
Standard arithmetic cannot be uniquely described (that is, described in a way that differentiates it from non-standard models) without giving a *non-computable* (not just infinite) amount of information.
Yet, you have described it as “standard arithmetic”, which is a finite and very small amount of information. You might argue that this information does not allow me, or anybody else, to derive/compute a complete axiomatic specification of standard arithmetic. OK, but if you use the term “standard arithmetic” AND state that it cannot have a finite specification, then you are relying on me to have the same intuition of “standard arithmetic” as you have, which does not look like a sound basis for discussion.
an infinite string of bits has infinite K.complexity
Sorry, that should have been: an infinite string of random bits.
You’ve also said repeatedly that simplicity, in this context, should be understood as having a short description. Now there are theorems galore saying that arithmetic has no short, or even finite, or even computable, description.
And there are computers, galore, that are capable of implementing arithmetic. They can implement addition, multiplication, subtraction, and division, and give the correct results. Yes, they fail at “correctly evaluating for truth the entire set of statements expressible ‘about’ arithmetic”. So something you can *do* with arithmetic is complex. But not arithmetic itself.
The fact is, that scientists have long resorted to math, including arithmetic, to describe theories, which in turn describe nature. Somehow, in doing so, they haven’t needed to specify anything of infinite complexity, because their descriptions of nature manage to be shorter than simply listing all observations.
The only way your purported insight can be true is by using non-standard definitions. But once we accept *those* definitions, your conclusions aren’t so interesting. (And now you see I’m not the only one noticing this.)
Kolmogorov Complexity is a concept that applies to strings of bits, not to mathematical objects. So it is a bit of an abuse of language to keep talking about the “K complexity of arithmetic”.
Then it’s just as much an abuse of language to speak of complexity of arithmetic, especially if you don’t even bother to spell out exactly what you mean by complexity. And the only analogous definition you’ve come up with is very far removed from the sense Dawkins was using the term in, when you tried to refute him. (Which is how this got started.) You simply don’t need an infinitely long specification to tell someone how to use arithmetic, which is the obvious relevant bit-string in this context.
Also, if you are (at least *now*) arguing that you’ve found an analog of K-complexity in your novel definition of complexity, then you agree the concept is applicable.
@Snorri_Godhi: OK, that’s fine, pace Silas Barta there are several definitions of complexity; e.g. there is computational complexity, which has nothing to do with K.complexity. But you need to make your notion of complexity measurable before you can argue that standard arithmetic is “very complex”.
You’re actually in agreement with me there. As I said in this comment there are more definitions, but a) K-complexity is the most relevant to the contexts he’s discussing, b) if he uses a different one, he needs to say so and make it well defined.
So let’s change that pace to a per ;-)
Silas:
Somehow, in doing so, they haven’t needed to specify anything of infinite complexity, because their descriptions of nature manage to be shorter than simply listing all observations.
A list of all observations has finite K.complexity.
Needless to say, this is off-topic, but [a] discussing these issues, it is best to keep on one’s toes and [b] it is of enormous relevance in another context, because it leads to Hume’s problem of induction.
The only way your purported insight can be true is by using non-standard definitions.
Non-standard definitions of what? of arithmetic, or of complexity?
As for Dawkins, I don’t see why anybody should bother to try to refute him.
A list of all observations has finite K.complexity.
Sure, but how does that detract from my point? I was saying that, by using arithmetic (in a scientific theory), you can (further) compress the (finite) space necessary to store all your observations. If Steven_Landsburg is correct, any use of arithmetic in an attempt to compress data would be futile, because the description of arithmetic (that you need to include in your model) would be infinitely complex, and fail to compress the data.
Non-standard definitions of what? of arithmetic, or of complexity?
Either and both. People normally believe you’ve described arithmetic when you’ve described how to do the operations +-*/ on numbers. Steven_Landsburg goes non-standard when he insists that you haven’t described arithmetic until you’ve generated *and* classified (as true or false) every statement expressible in arithmetic. But that’s confusing “the complexity of X” with “the complexity of judgments about everything you could potentially do with X”. (Analogous to confusing the complexity of a brick, with the complexity of a structure built with bricks.)
And, of course, even if you accept his definitions, you have to apply them consistently, which destroys their entire significance with respect to the point he was trying to make. Why am I supposed to be in awe at how “arithmetic” (as Steven_Landsburg defines it) has always existed, with maximal complexity? Because if arithmetic is “the set of classified statements expressible with basic operations on the natural numbers”, then in what sense does it actually exist? Where can I find it in the universe? (Or the multiverse?) To what observable structure is that set (the full set) isomorphic?
Ah, it only “exists” sort of as a potentiality without any, um, potential physical form. Now, what was all that about naturalism being true…?
As for Dawkins, I don’t see why anybody should bother to try to refute him.
Up to you, but Steven_Landsburg certainly did, which is what got him into this tangled mess.
And also to respond to the post:
But of course any sequence of arbitrary complexity sits inside the very simple sequence 010101010101….., if you can pick and choose what to keep and what to throw away. Complexity can reside quite comfortably inside simplicity.
No, it can’t. If you want to specify a sequence from “picking and choosing” from 01010101010101…, you have to specify both the repetitive 0101’s *and* the indices of all the values you want to use, when throws complexity on top of the simplicity of the pattern. Even in a nebulous, metaphorical sense, that comparison doesn’t work.
Silas:
If you want to specify a sequence from “picking and choosing” from 01010101010101…, you have to specify both the repetitive 0101’s *and* the indices of all the values you want to use, when throws complexity on top of the simplicity of the pattern.
YES! My point exactly! This is *precisely* why the natural numbers can sit inside the reals and still be more complex. If you want to describe the natural numbers, given the real numbers, you still have to specify which real numbers are natural numbers, which “throws complexity on top of the simplicity”.
As to this:
Steven_Landsburg goes non-standard when he insists that you haven’t described arithmetic until you’ve generated *and* classified (as true or false) every statement expressible in arithmetic.
I am running out of different ways to explain this. THAT’S NOT THE CRITERION I’M STARTING WITH. The criterion is that you haven’t described arithmetic until your description specifies it uniquely. (Analogous to saying that you haven’t described a brick if tell me only that it’s red.) There are *theorems* that say you have not met this criterion as long as your theory is incomplete in the Godel sense, and other theorems that tell you that any recursive description must be incomplete in the Godel sense. You can continue to ignore those theorems, but they won’t go away.
Silas: I mis- and under-estimated your position yesterday. Your original blog post did not seem to directly address the core of Steve’s argument. The following is much more to the point in my immodest opinion:
And there are computers, galore, that are capable of implementing arithmetic. They can implement addition, multiplication, subtraction, and division, and give the correct results. Yes, they fail at “correctly evaluating for truth the entire set of statements expressible ‘about’ arithmetic”. So something you can *do* with arithmetic is complex. But not arithmetic itself.
Yesterday I promised to start again from 1st principles, but the following is little more than expanding on [my interpretation of] the above paragraph.
First, as a nominalist, I do not believe that any statement expressible about arithmetic is necessarily true or false: it can also be indeterminate. (Am I really an intuitionist?) The only way to make every such statement true or false is to specify a unique model, which however would require a specification of infinite K.complexity. (I insist on K.complexity so as to exclude specifications of infinite length which are compressible to finite length.)
Next, I make a distinction. Peano arithmetic, or any arithmetic that can be implemented in digital computers, has finite K.complexity.
Platonic arithmetic, in which every purely arithmetical statement is either true or false, has infinite K.complexity but exists only as a theoretical possibility, in the same sense that an infinite string of random bits exists (also with infinite K.complexity).
In my increasingly immodest opinion, that disposes of the latest retort from Steve:
The criterion is that you haven’t described arithmetic until your description specifies it uniquely.
Steve’s criterion of “unique specification” seems to exclude Peano arithmetic and include platonic arithmetic — which, however, Steve has himself failed to specify uniquely, using instead an appeal to intuition.
But we can, and do, live without platonic arithmetic: Peano arithmetic is good enough for most practical purposes, and can be expanded ad hoc when needed. It is specified well enough for implementation in a mobile phone, with space left for a few (approximated) transcendental functions.
Snorri: Why do you keep saying that Peano arithmetic has finite K complexity? Any first order formulation of Peano arithmetic requires infinitely many axioms.
Why do you keep saying that Peano arithmetic has finite K complexity?
Because it’s implemented in my mobile phone, that’s why!
Any first order formulation of Peano arithmetic requires infinitely many axioms.
Ah, but that’s not the same as infinite K.complexity. The axiom schema from which the “smallest number” axioms are generated has finite K.complexity, and you can generate all of the infinitely many axioms from it (in an infinite amount of time, of course; but any “smallest number” axiom will be generated in a finite amount of time.)
Snorri: So can your mobile phone tell me whether every even number is the sum of two primes?
So can your mobile phone tell me whether every even number is the sum of two primes?
My mobile phone is not a general-purpose computer.
If there is a yes/no answer within Peano arithmetic, a general-purpose computer can find it when provided with the Peano axioms/schemata and rules of inference.
(Unfortunately, if there is no answer, then a GP computer might be unable to find that there is no answer.)
But I suppose that you have chosen this example because you believe that there is a “true” answer, even though it is not provable within Peano arithmetic. Am I right?
A correction to my comment from yesterday.
Steve:
The standard model is distinguished (within any given model of set theory, at least) by the condition that all models contain it as an initial segment.
Yours truly:
Am I correct to infer that all non-standard models have finite K.complexity?
I wrote that in a hurry (although long before opening the whisky bottle).
Re-reading it, I see that Steve’s comment implies that non-standard models are *more* complex than the standard model, not less. Sorry.
Snorri:
If there is a yes/no answer within Peano arithmetic, a general-purpose computer can find it when provided with the Peano axioms/schemata and rules of inference.
True, but only in the same sense that if your grandmother had wheels she would be a trolley car.
You are going to need either an infinite number of first order axioms, or a second order axiom schema together with a non-recursively-definable collection of rules of inference. Neither of which you will ever be able to feed to your general purpose computer.
You are going to need either an infinite number of first order axioms, or a second order axiom schema together with a non-recursively-definable collection of rules of inference. Neither of which you will ever be able to feed to your general purpose computer.
Again?
An axiom schema is an algorithm to decide in a finite amount of time whether any statement is an axiom or not: you said it yourself. So the axiom schema can definitely be fed into a computer.
Snorri: Yet again: Go ahead and feed your second order axiom schema into your computer. You still need to provide your computer with laws of inference. Good luck with that.
Steve: it was you who said that an axiom schema is an explicit, finite procedure to decide what is an axiom. You cannot escape the consequences of your own statement.
And incidentally, why are you shifting your ground?
Yesterday you wrote:
Peano arithmetic is not arithmetic. The existence of non-standard models (which satisfy the Peano axioms but which are not arithmetic) tells you that. My whole point here is that to describe *arithmetic* is far more difficult than to describe *Peano arithmetic*.
Today you are claiming that Peano arithmetic itself is non-computable. Is that because you have accepted that what you called *arithmetic* yesterday is a fiction?
Snorri: It is not enough to recognize the axioms. You also have to recognize the rules of inference. I’m not sure what’s been unclear about this.
Steve: you are dodging the hard question:
Why did you shift your ground from “arithmetic” to Peano arithmetic?
As for the trivial issue:
As you said in this post, introducing an axiom schema makes it possible to use 1st order logic. What more do you need to “recognize the rules of inference”?
FYI I just found out on wikipedia that Presburger arithmetic [a] has an axiom schema and [b] all its theorems can be derived algorithmically. That shows that axiom schemata are no impediment to algorithmic implementation.
Snorri: I am finding it harder and harder to follow your comments. I have no idea in what sense you think I’ve “shifted my ground”. The Peano axioms do not specify arithmetic. No set of axioms specifies arithmetic (where a “set of axioms” is required to be recursive). Your mobile phone, or your general purpose computer, provided with the Peano axioms and any other (true) axioms you care to add, is quite incapable of answering any question that would distinguish between one model of arithmetic and another. No matter how you program it, it cannot reliably tell you which polynomial equations are solvable in natural numbers; that’s a question *within* arithmetic that it cannot answer. Arithmetic is too complicated for your mobile phone and too complicated for your general purpose computer. And finally, the axiom schema of Presburger arithmetic generates a system of axioms with a *complete first order theory*, whereas the axiom schema of Peano arithmetic does nothing of the kind. The problem is not with axiom schemata per se; it is with an axiom schema that cannot generate a complete theory in the absence of second order rules of inference.
Not so fast! More paragraphing would help.
I have no idea in what sense you think I’ve “shifted my ground”.
Don’t worry, I will press on with it until you get a clear idea.
The Peano axioms do not specify arithmetic. […] Arithmetic is too complicated for your mobile phone and too complicated for your general purpose computer.
Now THAT was your original ground, and I am happy to see you return to it. The trouble is that your notion of “arithmetic” looks like a figment of your imagination: a mathematical theory which [a] can express elementary arithmetic, [b] is consistent, and [c] is complete.
I agree that this “platonic arithmetic” is not specified by the Peano axioms; and that is too complicated for my computer, not to mention my mobile phone. But of course it is: it is a figment of your imagination. And also Godel’s imagination, and Plato’s: you are in illustrious (however mentally unstable) company; but that makes your notion no less of a fantasy.
And finally, the axiom schema of Presburger arithmetic generates a system of axioms with a *complete first order theory*, whereas the axiom schema of Peano arithmetic does nothing of the kind. The problem is not with axiom schemata per se; it is with an axiom schema that cannot generate a complete theory in the absence of second order rules of inference.
OK, fine, Peano arithmetic is not complete. Who cares? the only way you can get a complete theory of arithmetic is if it is either inconsistent or a figment of your imagination, as I said above.
@Steve_Landsburg: YES! My point exactly! This is *precisely* why the natural numbers can sit inside the reals and still be more complex
And why the reals can sit inside the natural numbers and still be more complex. Oops, intransitivity of cardinality! Someone made a mistake somewhere …
I am running out of different ways to explain this. THAT’S NOT THE CRITERION I’M STARTING WITH. The criterion is that you haven’t described arithmetic until your description specifies it uniquely.
Well, we have working computers (which simulate universal Turing machines) that seem to have arithmetic uniquely specified for them. They never face ambiguity about what the output of a computation or program should be. What’s more, this capability can’t be an artifact of computers having some psychological commonality with humans that we’re implicitly relying on when we tell them what to do; programmers have to specify unambiguously what to do when they implement arithmetic. Computers have been directed to one and only one system.
There are *theorems* that say you have not met this criterion as long as your theory is incomplete in the Godel sense, and other theorems that tell you that any recursive description must be incomplete in the Godel sense. You can continue to ignore those theorems, but they won’t go away.
The theorems don’t prove the point you’re trying to make here; your claim that your argument reduces to some well-established theorems is just an attempt to divert attention from where your error is. The error is in the shifting of definitions while retaining the baggage of the old definitions, not in the theorems.
Please, watch what happens when you try to carry the same definitions of complexity and arithmetic all the way through:
1) Arithmetic is (by your definition) the uniquely specified set of truths about the natural numbers. (or something like that — my point still works)
2) Something is complex in proportion to the length of the description necessary to uniquely specify it.
3) Arithmetic has always existed.
4) Arithmetic cannot be described, even given infinite length.
–And now for the refutation of Dawkins–
5) Therefore, we have an example of something that has always been complex without arising from simpler origins.
See the problem? If you keep your definition of arithmetic through the whole thing, 3) ceases to be true! Arithmetic, by that definition, does not exist, if for no other reason that that the universe as we know it is computable, and you claim that arithmetic is not. Therefore, it cannot be isomorphic to any part or process of this universe. It doesn’t exist.
But, you might say, it exists kinda outside the universe, in a sort of immaterial Platonic space. Fine, but there goes your grounding in naturalistic, material explanations.
1) Arithmetic is (by your definition) the uniquely specified set of truths about the natural numbers. (or something like that — my point still works)
No, arithmetic (as I have consistently used the word) is the standard model of the natural numbers (with addition and multiplication).
2) Something is complex in proportion to the length of the description necessary to uniquely specify it.
No, it’s not just a matter of the *length* of the description; it’s also a matter of the recursivity. I have given you (about sixteen billion times, I think), the example of the real number system, which requires an infinite number of axioms but is still simpler than arithmetic.
3) Arithmetic has always existed.
Yes, this is certainly the crux of the matter. I (along with most mathematicians) believe this, though of course I (and they) could well be wrong. If this is the point you are disputing, fine—but then all your all other blather about arithmetic being simple is quite beside the point.
But, you might say, it exists kinda outside the universe, in a sort of immaterial Platonic space. Fine, but there goes your grounding in naturalistic, material explanations.
Yes, this is “kinda” what I might say. But why do you think this detracts from the counterexample to Dawkins? Dawkins says that all complexity must evolve from simplicity. I say that arithmetic is complex and did not evolve from anything simple. What do “naturalistic material explanations” have to do with it?
No, arithmetic (as I have consistently used the word) is the standard model of the natural numbers (with addition and multiplication).
No, that’s not your definition, because you disagree that proffered models of numbers implementing addition and multiplication — like those used on cell phones — aren’t arithmetic. But whatever. Let’s go with this; my point still holds.
No, it’s not just a matter of the *length* of the description; it’s also a matter of the recursivity. I have given you (about sixteen billion times, I think), the example of the real number system, which requires an infinite number of axioms but is still simpler than arithmetic.
Recursivity is a factor affecting the length of the (shortest) *necessary* description, and your comparison between the real and natural numbers relied on an intransitive metric, but whatever. Again, doesn’t affect the larger point, which I’ll get to below.
3) Arithmetic has always existed.
Yes, this is certainly the crux of the matter. I (along with most Platonists) believe this
There. Fixed that for you. It’s actually a contentious issue of what it means for “arithmetic” to exist, but those saying it necessarily “always” existed better identifies Platonists than mathematicians in general. (The only way in which arithmetic has always existed is in the sense that “manipulating stuff isomorphic to a system satisfying the axioms of arithmetic would have always yielded the arithmetically correct result when interpreting through the same isomorphism”. But this isn’t true for your definition of arithmetic because the counterfactual couldn’t ever have been met. But I digress…)
If this is the point you are disputing, fine—but then all your all other blather about arithmetic being simple is quite beside the point. … why do you think this detracts from the counterexample to Dawkins? Dawkins says that all complexity must evolve from simplicity. I say that arithmetic is complex and did not evolve from anything simple.
Do you really not see how these are all inter-related? What relates all of these terms is that whenever you consistently use the same definition of your terms throughout, you get an incorrect result. When it’s clear that math isn’t complex, you change up the definition of arithmetic to make it complex. But in doing so, you make it no longer meet the “exist” standard.
We have mechanisms that implement a uniquely-specified system of arithmetic. Those don’t count, you say — arithmetic refers to the standard model of + and x on the natural numbers, and you can’t *possibly* uniquely specify that in a computable way. So, you claim arithmetic is more than infinitely complex — it’s not even computable.
But oops — now that we’ve got the “arithmetic is complex” statement to be true, now we’ve destroyed the truth of the “arithmetic exists” claim, which again requires a nebulous, non-standard definition — this time of “exist” — to be true.
If arithmetic is really uncomputable, then nothing implements it, including and especially the universe. So it has never existed. Okay, so let’s broaden the definition of “exist” to “immaterial stuff that can’t be observed and doesn’t interact with the universe …”
Anyway, I hope you can see now why you’re leaving the realm of materialism. And how the supposedly different topics relate in that every time you try to salvage the truth of your claim in a novel definition of a term, you just force another of your terms to have an absurd definition.
Anyway, I hope you can see now why you’re leaving the realm of materialism.
If this was your point, you could have saved a lot of time (and avoid saying a lot of silly things) by stating it clearly upfront. Yes, of course the platonic world of mathematical objects is non-material. I’d have thought that was obvious.
I believe that the natural numbers exist in the platonic sense of existence. My book gives a lot of reasons why I believe that. You are entitled, of course, to believe otherwise.
Silas and Steve: contrary to you, I do not care less about Silas’ points [3] and [5]. (Or rather, the points that Silas attributes to Steve.) I do not care, because I see them as theological issues, and I am religiously agnostic.
What both of you seem to be missing is that there is a contradiction already between points [1] and [4]:
1) Arithmetic is (by your [Steve’s] definition) the uniquely specified set of truths about the natural numbers. (or something like that — my [Silas] point still works)
4) Arithmetic cannot be described, even given infinite length.
If arithmetic is uniquely specified, then it can be described; and if it cannot be described, then it is not uniquely specified.
The result still holds if we replace [1] with [1′]:
1′) arithmetic (as I [Steve] have consistently used the word) is the standard model of the natural numbers (with addition and multiplication).
The standard model is uniquely specified, therefore [1′] –> [1].
Silas: 2) Something is complex in proportion to the length of the description necessary to uniquely specify it.
Steve: No, it’s not just a matter of the *length* of the description; it’s also a matter of the recursivity. I have given you (about sixteen billion times, I think), the example of the real number system, which requires an infinite number of axioms but is still simpler than arithmetic.
Big mistake: Silas wrote: the length of the description necessary to uniquely specify it. The infinite axioms of the real field do not require an infinite description.
Snorri: Nothing requires an infinite description if you allow yourself the right vocabulary; give me any sequence of bits, I can name it “the Snorri sequence” and thereafter I can name it in three words. To get anything meaningful out of this notion of complexity, you have to commit yourself to a vocabulary *in advance*; it seems to me that the natural vocabulary in this case would be that of first-order logic.
Steve: have you ever heard of the 1st Law of Holes?
Nothing requires an infinite description if you allow yourself the right vocabulary
This is
[a] wrong [unless you allow for a vocabulary of infinite length];
[b] in direct contradiction of your earlier [also wrong] claim that the axioms of the real field require an infinite description;
[c] indicative of a misunderstanding of information theory.
Snorri:
This is
[a] wrong [unless you allow for a vocabulary of infinite length];
Actually, it’s trivially right if you read it the way it was intended.
You are reading it (I think) as: “There exists a vocabulary V such that for all X, X has a finite description in V.” What was intended was “For all X, there exists a vocabulary V such that X has a finite description in V.” The first is (as you note) obviously wrong; the second is obviously right.
[b] in direct contradiction of your earlier [also wrong] claim that the axioms of the real field require an infinite description;
The axioms of the real field require an infinite description provided you restrict yourself to first-order language. If you allow yourself to make up new languages as you go along, then you can invent a language in which they can be described in one word.
You are reading it (I think) as: “There exists a vocabulary V such that for all X, X has a finite description in V.”
Wrong.
What was intended was “For all X, there exists a vocabulary V such that X has a finite description in V.” The first is (as you note) obviously wrong; the second is obviously right.
No it isn’t. Not if X is an infinite string of random bits.
(NB: even a single infinite string of random bits requires an infinite-length vocabulary to assign it a finite description: I don’t need to include the entire uncountable set of all infinite strings of random bits.)
The axioms of the real field require an infinite description provided you restrict yourself to first-order language.
Let’s be clear on this, and let’s change subject to Presburger arithmetic if you don’t mind. Are you saying that the axiom schema of induction, together with first-order rules of inference, cannot be used to generate infinitely many axioms?
I’d appreciate a yes/no answer.
If this was your point, you could have saved a lot of time (and avoid saying a lot of silly things) by stating it clearly upfront. Yes, of course the platonic world of mathematical objects is non-material. I’d have thought that was obvious.
It takes a lot of time, because your error is in being consistent across 3-4 definitions. If you keep shifting your definitions, you can be correct on each issue, but won’t be consistent. And since (as I’m clearly not the only one to notice) you use non-standard definitions, you can keep wiggling out of any error by appealing to your definition, which then throws you off in one of your other claims.
That is why it appears to take a long time to find a simple disagreement.
***
Okay, so now the definition of “existence” that you use is referring to (at least) Platonic existence.
Now, let’s (once again) go back to how you were using the argument: to refute a point by Dawkins that complexity must arise from simplicity. You claim that this is not true, because infinitely complex math (which isn’t infinitely complex, as shown by all the computers that finitely specify a unique math, but whatever) has always existed.
See the problem? Dawkins was referring to complexity in a non-Platonic domain. Note how he *doesn’t* say, “‘Biological evolution is mathematically possible’ must have evolved.” — which would have to be his point for your appeal to existence in Platonic domains to be relevant. Rather, he says, “Biological beings must have evolved.” (the object- rather than meta-level)
In short, you took a statement referring to non-Platonic domains, and masterfully showed it to be false in Platonic domains. Is that supposed to be insightful?
Silas: the concept that you are trying to express is: fallacy of equivocation. I have more to say on this, but not now.
Silas:
1) your error is in being consistent across 3-4 definitions.
I’d be more inclined to attribute the problem to your unwillingness to read what I’ve actually said. I take complexity to be measured by the difficulty of specifying something uniquely in first-order language. Longer descriptions imply more complexity than shorter descriptions; non-recursive descriptions imply more complexity than recursive descriptions. This is, I claim, both reasonably precise and well within the spirit of what is usually meant by complexity.
2) Once again you say that arithmetic “isn’t infinitely complex, as shown by all the computers that finitely specify a unique math” whereas this is just plain untrue. For each of those computers, there is a purely arithmetical statement whose truth or falsity is undetermined by the specification. It follows that there are multiple, mutually incompatible models of arithmetic that are all consistent with what’s in your computer. In that sense, the math is not unique. Maybe you have some other definition of uniqueness in mind, but you haven’t shared it.
3) For someone who’s so concerned about definitions, I note that you still haven’t answered *my* question about what you mean when you say arithmetic is “simple”. (Here “arithmetic” means “the standard model of the natural numbers”, as it has throughout the discussion—at least in my posts.) You also haven’t specified what you mean by a “unique math”; the math is not unique in the sense of point 2) above, so in what sense *do* you think it’s unique? Repeat: What do you mean by simple? What do you mean by unique?
4) I’ve never seen Dawkins qualify his position with regard to domains of applicability. He makes a broad general statement that complexity, wherever it occurs, must evolve from simplicity. Arithmetic is a counterexample to that, unless you deny either that a) arithmetic exists or b) arithmetic is complex. If you deny a), then you are within your rights, but I disagree, for reasons I’ve expounded at length in my book; in this, for what it’s worth, I am on the side of most mathematicians (and, I daresay, most non-mathematicians as well). If you deny b), then you’re going to have to give me *your* definition of complexity, because it’s certainly complex according to mine (non-existence of a complete theory with a recursive set of first-order axioms).
Steve: I am waiting for a yes or no.
Snorri:
Are you saying that the axiom schema of induction, together with first-order rules of inference, cannot be used to generate infinitely many axioms?
I suppose this depends on what you mean by “generate”, but by any reasonable definition, the whole *point* of the axiom schema is to generate infinitely many axioms.
Snorri:
Here is what I think you and I are saying; you can let me know if you think I’m still misunderstanding you.
1) I say: I can define Peano arithmetic in two words: “Peano arithmetic”. I can define the standard model of arithmetic in five words: “The standard model of arithmetic”. But these “definitions” are cheats, because they don’t actually tell anyone how to discover the properties of Peano arithmetic or of the standard model. The problem here is that I have allowed myself to use a *language* that shouldn’t have been allowed. And by analogy, you can define Peano arithmetic via an axiom schema or the standard model via second order axioms—but that’s the same sort of cheat; you are stepping outside the default language of first-order logic.
2) You say: Hold on a minute. At least regarding Peano arithmetic, it’s not the same sort of cheat at all, because the axiom schema together with first order logic really does allow me to discover every theorem in Peano arithmetic. That’s a whole lot more informative than your two-word “Peano arithmetic” description, and it should count as a finite description.
3) I say: Touche. You are right that my analogy fails badly in this regard. On the one hand, you’ve “cheated” in the sense of allowing yourself non-first-order language; on the other hand, the cheat is arguably a harmless one. (On the other hand, let’s not lose sight of the fact that your ability to discover every theorem is not at all the same thing as the ability to take a given statement and discover whether it’s a theorem or not.)
4) I say further: However, Peano arithmetic is not arithmetic. This kind of cheat won’t work when it comes to defining the standard model; there you’re really stuck.
5) You say: I don’t care, because the standard model is a bit of metaphysical baggage that I don’t want to commit myself to anyway.
6) I say: I find it a little hard to take this seriously, in exactly the same way that I would find it hard to take seriously an assertion that you don’t believe in conscious beings other than yourself. But, as with that assertion, I certainly can’t prove you wrong.
Does the above misrepresent you?
I suppose this depends on what you mean by “generate”, but by any reasonable definition, the whole *point* of the axiom schema is to generate infinitely many axioms.
In answer to a yes/no question, this is technically defined as “weaseling out”.
Does the above misrepresent you?
Part of it does; part of it does not.
NB1: this is not weaseling out: I’ll answer yes or no wrt each of your points in due time.
NB2: that does not excuse you from providing a yes/no answer. When I smell blood, I don’t give up easily.
1) I say: I can define Peano arithmetic in two words: “Peano arithmetic”. I can define the standard model of arithmetic in five words: “The standard model of arithmetic”. But these “definitions” are cheats, because they don’t actually tell anyone how to discover the properties of Peano arithmetic or of the standard model.
You are introducing slippery language: what are these “properties” that you are talking about?
1a. As far as I am concerned, the properties of P.a. are all the theorems that can be deduced from it, and nothing more. Similarly for the standard model.
1b. Alternatively, and I think equivalently, the properties are those theorems that hold true for all arithmetic calculations that I can do with my computer (and a fortiori with my mobile phone).
The problem here […] the default language of first-order logic.
In view of my remarks above, this makes little or no sense.
2) [omitted for brevity]
That sounds right; except that your two-word description “Peano arithmetic”, in conjunction with the wikipedia article on the subject, is just as informative as my supposed “cheat”.
3) I say: Touche. You are right that my analogy fails badly in this regard. On the one hand, you’ve “cheated” in the sense of allowing yourself non-first-order language;
Have I allowed myself non-1st-order language? maybe I have, but where and when?
on the other hand, the cheat is arguably a harmless one.
First tell me where I cheated and then we can discuss whether it is harmless.
(On the other hand, let’s not lose sight of the fact that your ability to discover every theorem is not at all the same thing as the ability to take a given statement and discover whether it’s a theorem or not.)
I certainly have not lost sight of it, as you could easily find if you read again my previous comments.
4) I say further: However, Peano arithmetic is not arithmetic.
I shall return to this point when tackling your fallacies of equivocation.
This kind of cheat won’t work when it comes to defining the standard model; there you’re really stuck.
4a. “Cheat” is your word, not mine.
4b. By definition, P.a. by itself “won’t work when it comes to defining the standard model”.
However, IF the set theory defining the standard model can be encoded in a finite set of axioms, axiom schemata, and rules of inference, THEN the standard model, too, has a finite description (K.complexity).
IF otoh the standard model does not have a finite description, THEN you, not me, are really stuck if you try to define it.
5) [omitted for brevity]
On the contrary: afaik the standard model is an axiomatic system that I don’t much care about, but is not metaphysical because it has finite K.complexity.
6) [omitted]
In view of my answer to [5], this is irrelevant.
Snorri: I wrote:
I suppose this depends on what you mean by “generate”, but by any reasonable definition, the whole *point* of the axiom schema is to generate infinitely many axioms.
You wrote:
In answer to a yes/no question, this is technically defined as “weaseling out”.
My answer was an unequivocal yes, subject to your not being allowed to specify a bizarre definition of “generate” after the fact.
Have I allowed myself non-1st-order language? maybe I have, but where and when?
Your axiom schema cannot be stated in first order language.
On the contrary: afaik the standard model is an axiomatic system
The standard model is not an axiomatic system. If you think it is, then you’re doomed to miss (what I see as) the entire point of this discussion.
Snorri:
PS:
You wrote:
1a. As far as I am concerned, the properties of P.a. are all the theorems that can be deduced from it, and nothing more. Similarly for the standard model.
What on earth could it possibly mean to “deduce a theorem from the standard model”? You are throwing around quite meaningless phrases here.
WRT the yes/no question, I take note that you accept that Presburger arithmetic has finite K.complexity (as should be obvious from the fact that all its theorems can, in principle, be derived by a computer algorithm).
Now is there any reason why the same does not apply to any other complete mathematical theory, such as geometry or the real field?
This is another yes/no question, but I note that
[a] a yes answer should be motivated, and
[b] a no answer would defeat your answer to Silas’ point [2] @December 18, 2009, 5:48 pm.
Your axiom schema cannot be stated in first order language.
No? then Presburger arithmetic cannot be stated in 1st-order language? then its theorems cannot be obtained by a computer algorithm?
The standard model is not an axiomatic system. If you think it is, then you’re doomed to miss (what I see as) the entire point of this discussion.
What on earth could it possibly mean to “deduce a theorem from the standard model”? You are throwing around quite meaningless phrases here.
Maybe I am indeed missing the point, but as I said I smell blood.
However, unlike Silas, I am more concerned with cornering you than with scoring points, so I am moving more carefully than he does.
OK, the standard model is not an axiomatic system, but would you agree with the following:
[a] the standard model is defined within an axiomatic system for set theory;
[b] all statements provable in P.a. [theorems of P.a.] hold true within the standard model;
[c] some statements in the language of P.a. are true within the standard model, even though they are undecidable within P.a.
[d] some statements in the language of P.a. are undecidable within the standard model.
The statements in [b] and [c] I call “theorems of the standard model”. If I am speaking loosely, I apologize, but it does not sound meaningless to me.
If otoh I am wrong in any or all of [a] to [d], then tell me and I’ll try again. Maybe tomorrow: it’s getting late here.
Snorri: I cannot answer your new yes/no question without understanding it. As far as I am aware, Kolmogorov complexity is defined for bit strings, not for logical theories. I’ve been employing *analogues* of K complexity in this discussion, but if you’re going to ask a point-blank question about the K-complexity of something for which K-complexity is not defined, then of course I have no answer.
If you want to provide a formal definition of the K-complexity of a theory, then I’ll be happy to try to answer your questions about the K-complexity of particular theories, though of course once you give your definition we should both be able to work this out for ourselves.
As for this:
then Presburger arithmetic cannot be stated in 1st-order language? then its theorems cannot be obtained by a computer algorithm?
Presburger arithmetic is a theory. I don’t know what “stated” means for a theory. If you are asking whether it can be axiomatized in first-order language, then the answer is yes, but only if you are willing to allow infinitely many axioms. If you are asking whether its theorems can be obtained by a computer algorithm, the answer is yes.
What is the point of these questions?
Edited to add: I should have said, of course, that BY DEFINITION Presburger arithmetic has infinitely many first-order axioms, all but finitely many of which are instances of a single axiom schema.
Snorri:
[d] some statements in the language of P.a. are undecidable within the standard model.
The fact that you could even formulate this sentence is indicative of the depths of your confusion. What would it even MEAN for a statement to be undecidable within the standard model?
Steve: the definition of K.complexity of a mathematical theory should be trivially obvious. The K.complexity is the minimum number of bits that you need for the computer program that can generate all theorems of the theory (with each theorem being generated after a finite amount of time). This number of bits is, of course, relative to a universal computer; but since we are only concerned with the issue whether it is finite or not, the choice of computer is not an issue.
At the risk of stating the obvious, it makes no difference whatsoever whether the bits encode axioms or axiom schemata.
Since there are algorithms to generate all theorems of Presburger arithmetic, it is obvious that it has finite K.complexity.
Now you should be able to answer the question: does X have finite K.complexity?
Let me translate that for you: is there an algorithm that can generate all theorems of X, with each theorem generated after a finite amount of time?
I’d like answers when X is replaced by [a] the real field and [b] Peano arithmetic.
My claim is that both answers are affirmative.
The fact that you could even formulate this sentence is indicative of the depths of your confusion. What would it even MEAN for a statement to be undecidable within the standard model?
Strange that you should say that. I referred to statements being true within the standard model (in my points [b] and [c] @3:40pm, blog time). You raise no objection to that.
Now if you accept that statements can be true (or false) within the standard model, why do you take issue with my saying that they can be undecidable?
At the very least, you need to tell me unambiguously that you agree with [a], [b], and [c], before objecting to [d].
Snorri:
is there an algorithm that can generate all theorems of X, with each theorem generated after a finite amount of time?
I’d like answers when X is replaced by [a] the real field and [b] Peano arithmetic.
[a] is an absolutely meaningless question. The answer to [b] is yes.
Strange that you should say that. I referred to statements being true within the standard model (in my points [b] and [c] @3:40pm, blog time). You raise no objection to that.
Now if you accept that statements can be true (or false) within the standard model, why do you take issue with my saying that they can be undecidable?
This is like asking “If you accept that green and yellow are colors, why do you take issue with my saying that a trapezoid is a color?” I don’t know how to begin answering, because I’m not sure how deep your confusion goes. But let’s start here:
“Undecidable” is not an alternative to “true” or “false”. It is an alternative to “provable” or “not provable”. A meaningful statement must be either true or false.
I am going to bed, but first, a statement and a request.
The statement, in 2 parts:
[1] I take it that you now accept that all complete theories, such as those of the real field, have finite K.complexity.
[2] I take it that you now accept that Peano arithmetic has finite K.complexity.
The request: please tell me if I am correct in [a], [b], and [c] @3:40 pm, before we delve deeper into [d].
Give me approx. 12 hours for a reply.
Snorri:
[1] I take it that you now accept that all complete theories, such as those of the real field, have finite K.complexity.
Surely this is false. Consider a theory with a countable number of symbols a, b, c, etc. and a single equivalence relation, say R. (That is, we have axioms saying that R is reflexive, symmetric and transitive.) Consider the various statements aRb, aRc, aRd, etc. and randomly assign each of these to be either an axiom or a non-axiom. This theory is complete, but for almost any set of random assignments, it won’t be specifiable with a finite amount of data.
[2] I take it that you now accept that Peano arithmetic has finite K.complexity.
There is a computer program with a finite number of input bits that can generate all the theorems of Peano arithmetic. This is not only true, but nearly obvious: Because the symbols of the theory are countable, the set of finite strings is countable. You can order the strings, run through them in order, and examine them to see whether they are valid proofs; if so, retain their final lines to get your list of theorems.
[a] the standard model is defined within an axiomatic system for set theory;
The phrase “standard model” can refer either to the (standard) natural numbers or to the (usual) mapping from Peano arithmetic to the natural numbers. I’ve been consistently using the phrase in the former sense. Obviously, that is not defined within an axiomatic system for set theory, since people knew about it long before there *were* axiomatic systems for set theory.
[b] all statements provable in P.a. [theorems of P.a.] hold true within the standard model;
Meaningless as stated; true if repaired to the following: All theorems of P.A. translate, under the standard mapping, into statements true within the standard model.
[c] some statements in the language of P.a. are true within the standard model, even though they are undecidable within P.a.
Again, meaningless as stated; true if repaired. What you want to say (I think) is: Some undecidable statements in P.A. translate, under the standard mapping, into statements true within the standard model.
I think you should post some technical reference where readers can learn a bit more.
I was reading your 1st book the other day and some theorem caught my eye so I looked it up. With these posts the jargon is gone so I don’t know where to start to find out more.
Yours truly: I take it that you now accept that all complete theories, such as those of the real field, have finite K.complexity.
Steve: Surely this is false.
Indeed, it is. What I had in mind is all complete theories that have actually been axiomatized, such as Tarski’s axiomatizations of geometry and of the reals. Sorry.
Steve:
The phrase “standard model” can refer either to the (standard) natural numbers or to the (usual) mapping from Peano arithmetic to the natural numbers. I’ve been consistently using the phrase in the former sense. Obviously, that is not defined within an axiomatic system for set theory, since people knew about it long before there *were* axiomatic systems for set theory.
OK, time to discuss fallacies of equivocation.
Let’s start with the above. Let’s use the symbols [A] and [B] for your definitions above:
[A]: standard model = standard natural numbers
[B]: standard model = standard mapping from Peano arithmetic to [A]
(In a slight abuse of terminology, I shall refer to the formulas and the right-hand sides interchangeably.)
I note that you claim to have used [A] consistently.
You also claim that [A] is not defined within any axiomatic set theory”; since [B] depends on [A], I infer that [B] does not depend on set theory, either.
Next, let’s look at the 1st time you referred to “the standard model”:
The standard model is distinguished (within any given model of set theory, at least) by the condition that all models contain it as an initial segment.
Pardon me if I am confused! However, just to keep things straight, I refer to this definition as
[C]: standard model = the model of Peano arithmetic within set theory that is contained as an initial segment by all other models.
Next, you wrote:
No model of arithmetic, standard or non-standard, can be specified in a computable way.
On the face of it, this contradicts [C], but is compatible with either [A] or [B]. Much depends on the meaning of “specified”, however.
Please note that I am skipping all your mentions of “standard arithmetic” and “non-standard models” (unless accompanied by “standard model”).
Next, I find:
arithmetic (as I have consistently used the word) is the standard model of the natural numbers (with addition and multiplication).
and again:
“arithmetic” means “the standard model of the natural numbers”
This seems compatible with [B] and [C], but if you combine definition [A] with the above, you get: arithmetic is the standard model of the standard model. I infer that, once more, you cannot have meant [A] in the above sentence.
Subsequent mentions of “standard model” seem compatible with [A]. But, if you always mean [A], why mention “the standard model” at all?? just say “the natural numbers”, consistently!
Snorri:
(1)
The standard model is distinguished (within any given model of set theory, at least) by the condition that all models contain it as an initial segment.
The parenthetical phrase here is superfluous; I’m sorry if I confused you by including it.
(2) On the face of it, this contradicts [C].
No it doesn’t.
This seems compatible with [B] and [C], but if you combine definition [A] with the above, you get: arithmetic is the standard model of the standard model. I infer that, once more, you cannot have meant [A] in the above sentence.
“The standard model”, “the standard model of the natural numbers”, “arithmetic”, and “the natural numbers” all refer, by standard conventions and slightly ambiguoously, to both [A] and [B], though I have tried to use them consistently to mean [A].
Subsequent mentions of “standard model” seem compatible with [A]. But, if you always mean [A], why mention “the standard model” at all??
To avoid any possible ambiguity. When I say “the natural numbers” I always mean [A]; sometimes I say “the standard model of the natural numbers” just in case someone thinks I mean “some arbitrary model of the natural models”. All of this is perfectly (pardon the pun) standard terminology. There is no ambiguity and no internal contradiction.
Snorri:
Steve: Surely this is false.
Indeed, it is. What I had in mind is all complete theories that have actually been axiomatized, such as Tarski’s axiomatizations of geometry and of the reals. Sorry.
Snorri: ALL theories have been “axiomatized”; that’s what a theory IS.
Steve: ALL theories have been “axiomatized”; that’s what a theory IS.
Have they? Fortunately, I can cut+paste to answer the question.
Consider a theory with a countable number of symbols a, b, c, etc. and a single equivalence relation, say R. (That is, we have axioms saying that R is reflexive, symmetric and transitive.) Consider the various statements aRb, aRc, aRd, etc. and randomly assign each of these to be either an axiom or a non-axiom.
Has this theory been axiomatized? You have defined the procedure to axiomatize it (assuming that you have a true-random bit generator), but I would not say that it is axiomatized until the infinite sequeence of random bits has actually been generated.
In invoke the 1st Law of Holes once more.
WRT [C]:
The parenthetical phrase here is superfluous; I’m sorry if I confused you by including it.
Not so fast: by defining the “standard model” in [C] as “the initial segment of all models” you have provided a unique description of it. That raises the question: a unique description in which language? in the language of set theory? but then, the parenthetical phrase is no longer superfluous.
In addition, the unique description of the standard model as the initial segment etc. contradicts your claim that [A] cannot be uniquely specified; and if [A] cannot be uniquely specified, then neither can [B].
“The standard model”, “the standard model of the natural numbers”, “arithmetic”, and “the natural numbers” all refer, by standard conventions and slightly ambiguoously, to both [A] and [B], though I have tried to use them consistently to mean [A].
That is saying:
* “The standard model”,
* “the standard model of the natural numbers”,
* “arithmetic”, and
* “the natural numbers”
all refer to both
– the natural numbers and
– the mapping from Peano arithmetic to the natural numbers,
though I have tried to use them consistently to mean
+ the natural numbers.
That is not just circular: it is a spaghetti junction in which you always end up at the starting place.
NB: I am just deconstructing here, but I have in mind a Socratic dialogue that should provide a better basis for further discussion. Shall I send it to you by e-mail?
Some nitpicking about your terminology from yesterday:
“Undecidable” is not an alternative to “true” or “false”. It is an alternative to “provable” or “not provable”.
I would label “undecidable” a statement that is unprovable, and whose negation is also unprovable. All of this within an axiomatic system, of course. So it is not an alternative to unprovable.
A meaningful statement must be either true or false.
That is a definition of “meaning” that I find extremely unpalatable. “Mary had a little lamb” makes perfect sense to me, even though, without specifying which Mary it refers to, it cannot be either true or false.
Has this theory been axiomatized?
Given that “axiomatized” is a meaningless word you just invented, I suppose you’re the only person who can answer this question.
Not so fast: by defining the “standard model” in [C] as “the initial segment of all models” you have provided a unique description of it. That raises the question: a unique description in which language? in the language of set theory? but then, the parenthetical phrase is no longer superfluous.
This is only a “description” if you first describe all models of set theory. Good luck with that.
If this is counts as a “description” of the natural numbers, then “the greatest thing in the Universe” counts as a description of God.
That is a definition of “meaning” that I find extremely unpalatable. “Mary had a little lamb” makes perfect sense to me, even though, without specifying which Mary it refers to, it cannot be either true or false.
That’s because it contains the unbound variable “Mary” and is therefore not a statement. Now you’re going to tell me that you don’t like this definition of “statement” and that by invoking it I’ve committed the fallacy of this, that or the other thing.
That is saying:
* “The standard model”,
* “the standard model of the natural numbers”,
* “arithmetic”, and
* “the natural numbers”
all refer to both
– the natural numbers and
– the mapping from Peano arithmetic to the natural numbers,
though I have tried to use them consistently to mean
+ the natural numbers.
That is not just circular: it is a spaghetti junction in which you always end up at the starting place.
It is perfectly standard terminology, and if you don’t like it, your beef is not with me; it’s with the way language happens to have evolved. If you don’t understand it, I’m perfectly happy to explain it to you. If you’re going to blame me for the fact that you don’t like it, I think we should end this discussion.
If this is counts as a “description” of the natural numbers, then “the greatest thing in the Universe” counts as a description of God.
Wrong analogy, for 2 reasons. The greatest thing in the Universe is, obviously, the Universe itself. But YOUR definition [C], not mine, of the standard model, is analogous to “the smallest thing in the Universe”.
That’s because it contains the unbound variable “Mary” and is therefore not a statement. Now you’re going to tell me that you don’t like this definition of “statement”
Actually I don’t like your definition of “unbound”. But that’s beside the point, since we are discussing a priori statements and my example was a posteriori. The point is that I reject out of hand your definition of “meaning”.
It is perfectly standard terminology, and if you don’t like it, your beef is not with me; it’s with the way language happens to have evolved.
I’ll believe it when you show me a refereed, published paper (not necessarily authored by you) which uses all of the above terms to refer to the same concept. I would settle for a set of papers, each of which uses 2 or more of the above terms to refer to the same concept; provided that the papers, taken together, establish the equivalence of the entire set of terms.
@Steve Landsburgh: As a person with an amateur interest in economics, I stumbled across your blog after following Mankiw’s link. I saw the discussion of arithmetic, and as a mathematician specializing in model theory, prepared to cringe. Yet reading your replies to Snorri Ghodi, no cringes occurred.
Is training in mathematical logic standard for economists? I’m really quite impressed.
But YOUR definition [C], not mine, of the standard model, is analogous to “the smallest thing in the Universe”.
[C] is not a definition; it’s a theorem.
Actually I don’t like your definition of “unbound”.
Yes, I know. This is only one of many standard definitions you don’t like, and are prepared to blame me for.
I’ll believe it when you show me a refereed, published paper (not necessarily authored by you) which uses all of the above terms to refer to the same concept.
Oh for Christ’s sake. If you don’t trust my knowledge of this subject, why are you asking me to explain it to you in the first place? Pick up any textbook on model theory. I’m done here.
Clifton: Thanks for this. Though you’d never guess it from this thread, Snorri has proved himself, elsewhere on this blog, to be capable of thoughtful and interesting commentary.
@Steve_Landsburg:
1) your error is in being consistent across 3-4 definitions.
I’d be more inclined to attribute the problem to your unwillingness to read what I’ve actually said.
And I’d be more inclined to an excessive willingness to read what you’ve said. See, when you use (or, as is more often, imply) a definition, I keep checking back to see that that definition hasn’t subtly shifted to carry over baggage from another meaning. I already read your original definition of complexty — there wasn’t one, just a mass of contradictions if I try to apply any one of them. Your reply contains a great example:
I take complexity to be measured by the difficulty of specifying something uniquely in first-order language. … For each [computer], there is a purely arithmetical statement whose truth or falsity is undetermined by the specification. … you still haven’t answered *my* question about what you mean when you say arithmetic is “simple”.
Okay, so you use “arithmetic” in a broader sense, in which existing computers aren’t implementing or describing it. Strange, but let’s go with that. Then you go on later to talk about how effective arithmetic is at understanding the world around us. But that’s a different meaning: it’s referring to a finitely-describable, computable system. So the system can’t distinguish whether it’s the system that has all numbers as the sum of two primes? So what? It doesn’t need to, and neither do models of the universe’s physics. The universe’s physics don’t contain anything uncomputable, so where’s the uncomputable arithmetic?
And I did explain what it means for arithmetic to be simple: you can finitely describe how to perform the arithmetic operations. You *must* be able to, else, using math in physics would have no data-compressive power.
(I find it strange that you never defined complexity originally, you never before thought about how the standard definition of complexity applies to the domain you were dealing with, and yet you still feel confident your original claims reached crucial insights related to complexity.)
I’ve never seen Dawkins qualify his position with regard to domains of applicability. He makes a broad general statement that complexity, wherever it occurs, must evolve from simplicity.
He quite clearly did qualify its applicability, since he was speaking about the material, observable world. And I already explained what he would have to be saying to mean it in any other sense (note the nested quotation): “‘Biological evolution is mathematically possible’ must have evolved.” Now, has Dawkins said, *anywhere* else, anything about the varying time-history of the theoretical mathematical possibility of biological evolution? Of course not: he makes claims about biological evolution, not about the evolution of the Platonic math behind biological evolution.
It’s begging the question to count the immaterial, undescribable Platonic realm, with no influence on this world, as a kind of existence qualitatively the same as that in the observable realm It’s another fallacy of equivocation: massively explain what counts as “existing”, and act like the looser kind has the same significance as the stricter kind.
Arithmetic is a counterexample to that, unless you deny either that a) arithmetic exists or b) arithmetic is complex. If you deny a), then you are within your rights, but I disagree, for reasons I’ve expounded at length in my book; in this, for what it’s worth, I am on the side of most mathematicians (and, I daresay, most non-mathematicians as well).
It “exists” in a fundamentally different sense than how you otherwise use the term, as I explained. Your only substantiation for your claim about mathetmaticians is your say-so.
You seem to be confusing a mathematical claim with an ontological one: believing in the counterfactual validity of mathematical claims, with their existence as fundamental entities. That is a subtle form of the mind projection fallacy, in that you’re equating your cognitive system’s recognition of similarity across domains (in that they all represent math somehow) with fundamental reality.
Though you’d never guess it from this thread, Snorri has proved himself, elsewhere on this blog, to be capable of thoughtful and interesting commentary.
Yes, he’s capable of thoughtful commentary, but somehow became a half-competent idiot on precisely this issue. Funny how that works out.
Steve: thank you for your kind words. (No offense taken for your other words: if we had to argue kindly here, it would cramp my style. You argue cogently, and that makes it worthwhile for me to argue with you — whether you like it or not.)
But I am uneasy that you consider thoughtful what I consider trivial, compared to my getting you to provide a reasonable* answer:
http://www.thebigquestions.com/2009/12/17/non-simple-arithmetic/#comment-1311
to the question that you yourself put to Silas:
http://www.thebigquestions.com/2009/12/17/non-simple-arithmetic/#comment-1295
Your answer is also an implicit admission of what I called your big mistake:
http://www.thebigquestions.com/2009/12/17/non-simple-arithmetic/#comment-1287
and it is also a retreat from shifting your ground:
http://www.thebigquestions.com/2009/12/17/non-simple-arithmetic/#comment-1256
Silas: Thank you for what I take as kind words, thinly disguised. Though it is strictly true that, in this issue, I am half-competent at best.
My further thoughts on this, if any, by e-mail only. I might cc to Silas. Neither of you should hold his breath.
* not quite the same answer as Silas gave today; but since the question is about a definition, there is no single correct answer.
@Snorri_Godhi: Thanks for your contributions to this discussion. As you inferred, I didn’t mean to insult you with my last comment about you — I was just pointing out to Steve_Landsburg why it would be strange to be so dismissive of your points.
In any case, the joke’s on us: Steve_Landsburg will continue to collect royalties on a book built from an inconsistent and haphazardly-constructed foundation. I can’t claim to be able to pull that off!
Hello, Dr. Landsburg;
Have you discussed any of these things with abstract algebra people?
the natural numbers are simple in abstract algebra, if I remember correctly, which I might not. In any case that’s not what I’m commenting about.
“A string of a million random numbers is complex, because it takes a long time to describe all of the content.”
the string of random numbers is described within the very statement you make, and so it does not take a long time to describe. One needs to differentiate between systems and projections thereof, that may be quite a bit more simple. That is, you don’t need to list the entire set to describe them.