A little while back, I posted the first half and then the second half of the honors exam in economics that I administered at Oberlin College. Since then, I’ve slowly doled out a few answers, but I’m getting more and more requests for the complete set. Here, then, are the questions and answers for the first half; I warn you that some of these are pretty technical. I’ll post the second half soon.
Question 1. When the price of peanuts rises, Frieda reduces her root beer consumption. If Frieda’s income rises, will her root beer consumption go up or down?
Answer: When the price of peanuts rises, two things happen that might affect Frieda’s root beer consumption: First, the relative price of root beer has fallen, which makes her consume more root beer. (Economists call this the substitution effect.) Second, Frieda feels poorer, which could make her consume either more or less root beer. (Economists call this the income effect.) Since the substitution effect is positive (i.e. it leads to more root beer) and the sum of the two effects is negative, we can infer that the income effect is negative. In other words: Frieda’s root beer consumption moves in the same direction as her income. So if her income rises, her root beer consumption goes up.
The Most Common Wrong Answer: When the price of peanuts rises, Frieda feels poorer and consumes less root beer. Therefore her root beer consumption moves in the same direction as her income, so when her income rises she consumes more root beer.
This is wrong, because it assumes that when the price of peanuts rises, Frieda feels only an income effect. A correct answer must account for the substitution effect as well.
Question 2. Bananas cost $6 apiece, except for members of the banana club, who pay $2 apiece.
- Given full knowledge of Thomas’s preferences, explain how you’d compute his willingness to pay for a membership in the banana club.
- Given knowledge only of Thomas’s demand curve for bananas, explain how you’d estimate his willingness to pay for a membership in the banana club.
- Under what circumstances is your estimate an overestimate? Under what circumstances is it an underestimate?
Answer (this one is technical!):
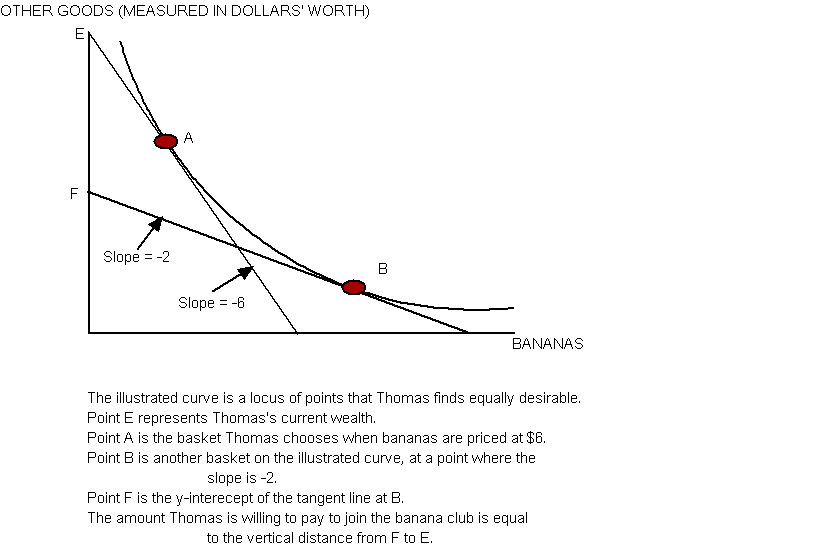
- Given full knowledge of Thomas’s preferences, you can first predict how many bananas he buys (and how much money he has left over) at the current $6 price. Now identify another combination of bananas-plus-other-goods that satisifies two conditions: a) Thomas likes it exactly as much as he likes his current basket and b) If Thomas owned this basket and bananas were priced at $2 each, he’d neither want to buy or sell bananas. Finally, compute the amount of money you’d have to take from him so that if bananas were priced at $2 each, he could just afford this latter basket. Here is the (technical) diagram that illustrates this answer. (Click the picture for higher resolution):
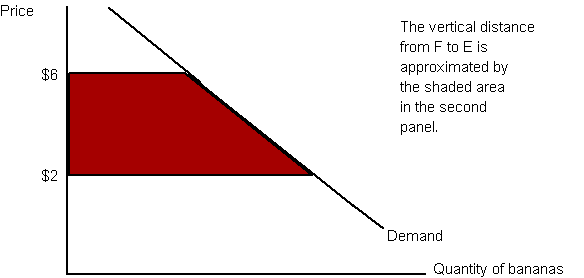
- You can approximate Thomas’s willingness to pay as the area bounded by his demand curve, the $6 price, and the $2 price, i.e. the shaded area here:
- If bananas are a normal good, the area is an underestimate; if bananas are an inferior good (i.e one that Thomas consumes less of when his income increases), the area is an overestimate.
Question 3. Snidely Whiplash owns all the grocery stores and all the houses in the Yukon Territory. He charges a competitive price for groceries, and rents the houses at the highest price residents (who are all identical) are willing to pay. (If he charged any more, they’d all leave town). True or False: If Snidely raises the price of groceries, he’ll have to lower the price of housing, so he’ll be no better off than before.
Answer: I’ve answered this one here.
Question 4. Discuss the consequences for economic efficiency of giving your father a Barnes and Noble gift card, under various assumptions about how he uses (or doesn’t use) the card.
Answer: If he doesn’t use the card at all, or if he uses it to buy books he’d have bought anyway, then the transaction is perfectly efficient. (When he doesn’t use the card, wealth is transferred from you to Barnes and Noble; when he uses it to buy books he’d have bought anyway, wealth is transferred from you to your father; in neither case is any wealth destroyed.)
If he uses a $50 card to buy books he wouldn’t otherwise have bought (because, for example, they were worth only $30 to him) then the simplest answer is that the transaction is inefficient because $50 worth of resources have been devoted to giving your father $30 worth of pleasure. On the other hand, this is so only if you believe the $50 book price accurately reflects the costs of production; if publishers have some monopoly power, this might not be true.
Question 5. Rank these taxes in order of how much you’d dislike paying them:
- A tax on consumption
- A tax on wages
- A tax on income (including wages, interest and dividends)
Assume that the tax rates are adjusted so that your total tax bill is the same in each case.
Answer: I’ve answered this one here.



Re your answer to #1, you note:
“The Most Common Wrong Answer: When the price of peanuts rises, Frieda feels poorer and consumes less root beer. Therefore her root beer consumption moves in the opposite direction from her income so when her income rises she consumes more root beer.”
Shouldn’t “opposite” in the penultimate line read “same”?
Concerning Q4: “Discuss the consequences for economic efficiency of giving your father a Barnes and Noble gift card, under various assumptions about how he uses (or doesn’t use) the card.”
This assumes, I think, the idea is to discuss the consequences for economic efficiency of giving a B&N gift card AS OPPOSED TO giving cash (how jejune!) or giving nothing at all (how caddish!). If you compare the economic efficiency of giving a B&N gift card to giving your father B&N books, then you have to assess the probability of your choosing for him books he values more than the cover price vs his doing so.
But I suspect this isn’t in the spirit of the question…
Thank you for the answers. I waited for them without pressing you, but now you know what is coming:
Could we get a diagram to go with answer #1 please?
Incidentally, answer #1 does not take into account another possible factor: Frieda only drinks root beer while eating peanuts.
WRT answer #2: of course, that is an upper bound on the membership fee that Thomas would pay. I would not pay a membership fee if the result is that I am exactly as satisfied as before.
Ross (re question #1):
Shouldn’t “opposite” in the penultimate line read “same”?
Excellent catch! Thank you. I’ve fixed this.
Re #1: What if (root) beer and peanuts are complements in consumption? This seems realitic, and then root beer may be a normal good. Reading the question on your actual test makes clear the important caveat that Frieda consumes ONLY these two goods, but I do not see how that could be gleaned from the wording here.
Blink:
You’re right; this was in the original exam and I failed to carry it over when I posted the questions here. Mea culpa.
Because of the diminishing return on wealth, shouldn’t the efficiency of not using the gift card in #4 depend somewhat on the wealth of my father as compared to the aggregate wealth of the B&N investors? Or is $10 worth exactly as much to Bill Gates as it is to an African child living in poverty?
Ben: The efficiency criterion (by definition) counts $10 to Bill Gates exactly as much as $10 to an African child living in poverty. So there is no ambiguity about what the efficiency criterion prescribes. A related but different question is: Why should we care what the efficiency criterion says? I’ve tried to answer this (in fact with specific reference to Bill Gates) on pages 166 to 168 of The Big Questions. The answer is a little subtler than you might guess.
Is the term ‘efficiency’ in economics limited to units of dollars? Why not extend the idea of efficiency to utility, which is definitionally more useful? In this paradigm, one would worry about destroying utility generally rather than destroying wealth specifically. When a policy causes $10 to be transferred from the poor to Bill Gates, your efficiency criterion says that nothing bad has happened while the utility efficiency idea says that something bad has happened. Clearly the latter is more in line with what practically everyone believes; shouldn’t that mean it is a more useful tool for making these types of decisions?
I’m not sure how Gates’ loud music applies here; that is a good argument for indulging the whims of those who control resources while this is a question of whether pure transfers are always to be considered neutral.
Why not extend the idea of efficiency to utility, which is definitionally more useful?
Actually, it is definitionally most useful to have different names for different concepts. Utility maximization is one thing; efficiency is another. It’s good to keep them straight.
I think strictly speaking the answer to the Frieda question — “If Frieda’s income rises, will her root beer consumption go up or down?” — should be “not enough information given” if you don’t know how much her income increases by.
You can draw indifference curves such that if the price of peanuts rises, Frieda reduces root beer consumption, and then if her income goes up by some amount, her root beer consumption goes up. On the other hand, you can also draw indifference curves such that if the price of peanuts rises, Frieda reduces root beer consumption, and then if her income goes up by some amount, her consumption of root beer goes *down*.
Example from real life: If the price of pork-flavored Ramen noodles goes up, a college student will increase their consumption of beef-flavored Ramen noodles. However, once the student graduates and their income goes (way) up, their consumption of beef-flavored Ramen noodles will often drop to zero as they start eating real food.
Would I be correct in assumping that the question should more precisely say, “Given a small positive delta change in Frieda’s income, will her root beer consumption go up or down by a small delta amount?” (Rather than asking how Frieda’s root beer consumption will change given an arbitrarily large change in Frieda’s income.)
Bennett: Yes, the implicit assumption in all these problems is that we’re talking about small changes.
Definitionally, utility refers to stuff that people value, so it must be more useful in determining people’s preferences than just production. One of the things I most admire about your writings is your ability to explain why it’s reasonable, proper and useful to measure utility in dollars, but what you seem to be saying here is that utility is entirely separate from dollars and the idea of efficiency entirely disregards utility (except when dollars and utility happen to coincide). Therefore, the way to defeat any policy argument based on efficiency is to show how, in that particular case, utility differs from dollars. That seems like an easy bar, particularly in the case of free trade.
Are you assuming that Frieda’s utility function (as a function of root beer and peanuts) is differentiable?
If not, then you can make indifference curves like these:
http://www.peacefire.org/peanuts-and-root-beer.jpg
In that curve, if the price of peanuts rises, then Frieda consumes less root beer. But if her income goes up, her root beer consumption goes down. On the other hand, in my graph, if her income goes *down*, her root beer consumption goes down as well.
Presumably when you say “Frieda’s root beer consumption moves in the same direction as her income,” that’s where you’re assuming it’s differentiable — that if her income moving one direction causes her root beer consumption to move one way, then her income moving in the opposite direction must cause her root beer consumption to move the opposite way.
Coming up with bizarre counterexamples is fun :)
Bennett: Nice counterexample, though as you surmise the implicit assumption (that we train our students always to make unless they have a good reason to doubt it) is that the utility function is twice continuously differentiable.
Ok thanks!
But, this is weird, what if you have an indifference curve like this:
http://www.peacefire.org/peanuts-and-root-beer.2.jpg
That’s still logically conceivable under the rule that utility has to be nondecreasing if your amount of either good increases… And even if the utility function has to be twice differentiable, I think you can still have two-humped indifference curves (can’t you?).
Then you can make the surrounding curves such that if Frieda’s income increases, she stays on one hump, but if her income decreases, she jumps to the other hump.
Then her utility function is twice differentiable, but the amount of root beer she purchases, as a function of income, is not even a continuous function. (And then you can structure the curves so that if the price of peanuts increases, she consumes less root beer, but if her income goes up, her root beer consumption could either increase or decrese.)